Предмет: Алгебра,
автор: nemoy99
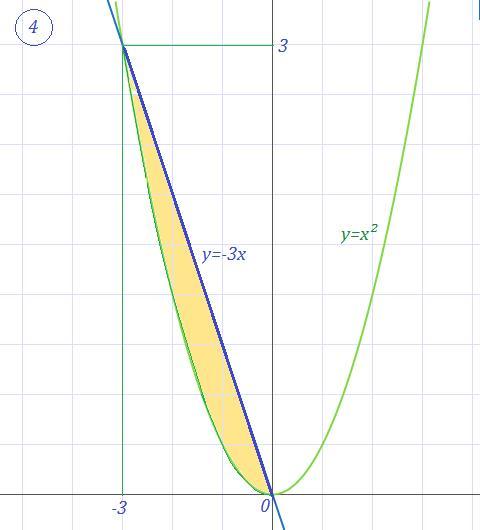
Вычислить площади фигур, ограниченных указанными линиями
Приложения:
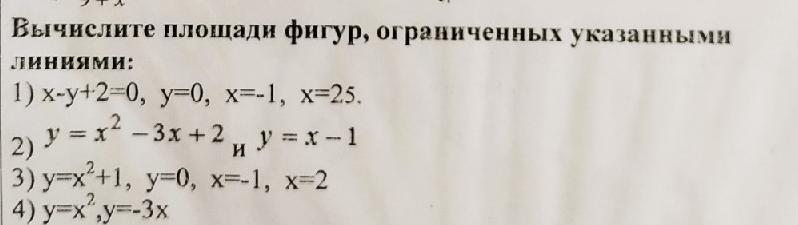
Ответы
Автор ответа:
0
Приложения:
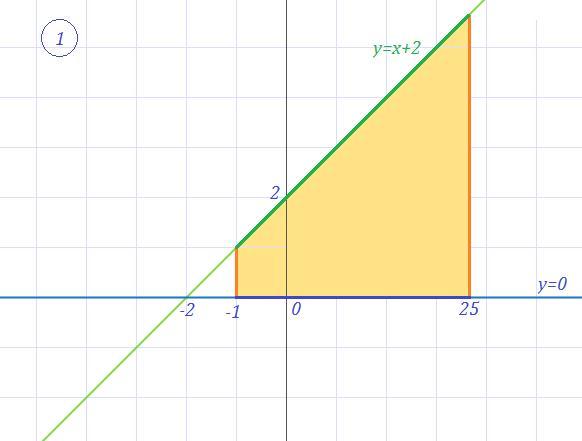
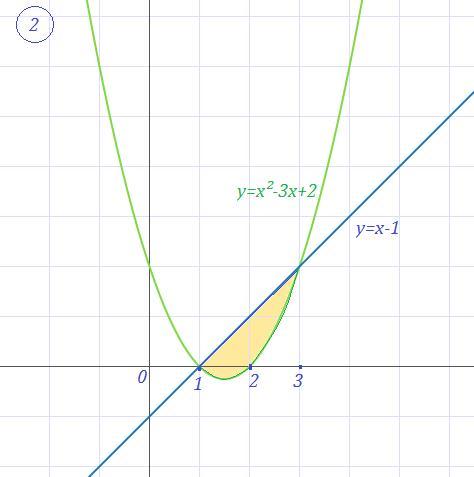
Похожие вопросы
Предмет: Математика,
автор: ogrizota1664
Предмет: Математика,
автор: malaya6951
Предмет: Алгебра,
автор: kavtop7180
Предмет: Математика,
автор: NagibatorIDITENAXYU
Предмет: История,
автор: lopux997