Помогите...........

Ответы
37. Пусть сторона основания а, тогда высота h основания равна а√3/2, а радиус вписанной окружности равен r=(1/3)h=(a√3/2)*(1/3)=
a√3/6, по условию это √3⇒а=6, тогда площадь правильного треугольника, площадь основания а²√3/4=36√3/4=9√3/см²/
Объем пирамиды равен v=(1/3) s*H=(1/3)9√3H=3√3*Н
H-высота пирамиды, она равна √((2√7)²-(√3)²)=
√(4*7-3)=√(28-3)=√25=5,объем равен 3√3*5=15√3/см³/
38. Найдем высоту пирамиды √((√37)²-(2√3)²)=√(37-12)=5, пусть сторона основания равна а, тогда высота основания а√3/2, а радиус описанной окружности равен (2/3)*(а√3/2)=а√3/3, по условию а√3/3=2√3⇒а=6/см/,
Площадь основания равна а²√3/4=36√3/4=9√3/см²/, тогда искомый объем равен (1/3)*9√3*5=15√3/см³/
39. Т.к. материал один и тот же, то плотность у них равная, все зависит от объема, масса той модели меньше, у которой меньше объем. Радиус шара равен 12см/2=6см=0.6дм
Объем куба равен 1 дм³, а шара посчитаем по формуле 4пr³/3=
4п*0.6³/3= 4п*0.216/3= 0.288п/дм³/примерно равен 0.9дм³, что меньше, чем объем куба. Поэтому масса шара меньше.
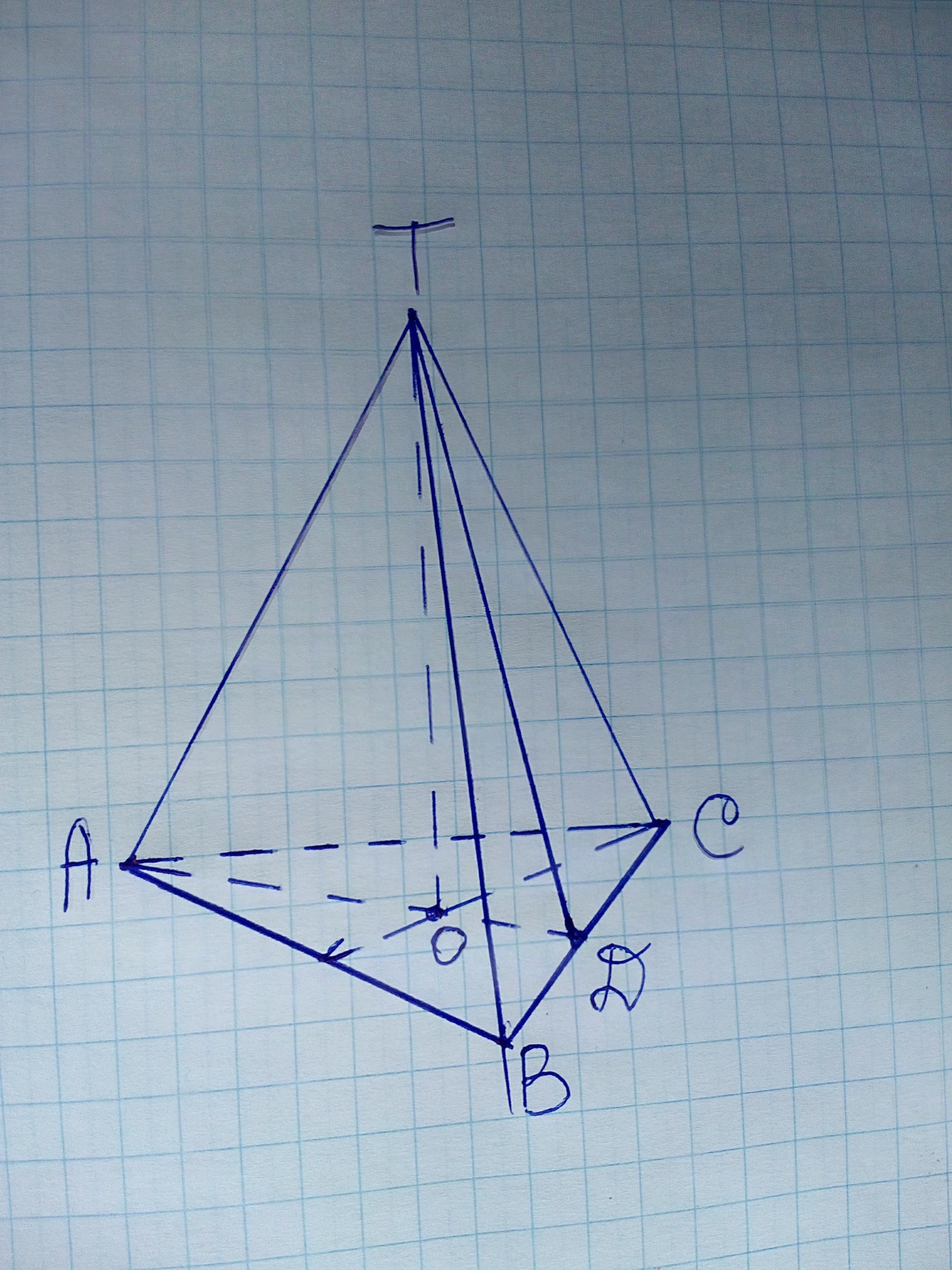
Дополняю рисунком свой ответ. По рисунку ТО- высота пирамиды, h=АД- высота основания, т.е. высота треугольника АВС, ТД- апофема, r=ОД- радиус вписанной в основаание пирамиды окружности, АО=R- радиус описанной около основания окружности. Рисунок годен к задачам 37; 38.