Предмет: Алгебра,
автор: DagyBagy
Нужно решить с помощью подстановки.
Приложения:
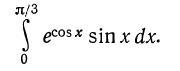
mathgenius:
внести синуc под дифференциал.
сos(x)=t . Вот вам и замена.
Вы верно поняли. Именно в этом и есть замена. Но ее понимают буквально- формально. Хотя пользуются не задумываясь.
Ответы
Автор ответа:
1
dcosx=-sinx*dx
-∫e^(cosx)d(cosx) пришли к табличному. ОН равен e^(cosx) верхний предел равен π/3, нижний 0, по Ньютону - Лейбницу
он равен -(е¹/²-е¹)=е-√е
2способ. Пусть соsx=в, тогда получим новые пределы интегрирования. Нижний предел 1, верхний предел 0.5.
-∫еᵇdв=-еᵇ; с учетом формулы Ньютона - Лейбница
получим -(е¹/²-е¹)=е-√е
Спасибо, Correlation показал более подробнее, т.к в этой теме я затупок.
))))))))))
Автор ответа:
4
по сути... это одно и то же. Я подставлял дифференциал от косинуса. а подведение под знак дифференциала - это всего лишь уловка выйти на табличный.
Похожие вопросы
Предмет: Математика,
автор: zxc770
Предмет: География,
автор: ashirbek660206
Предмет: Биология,
автор: k1nver
Предмет: Математика,
автор: optovka2008
Предмет: Математика,
автор: marena5