Question

Помогите решить
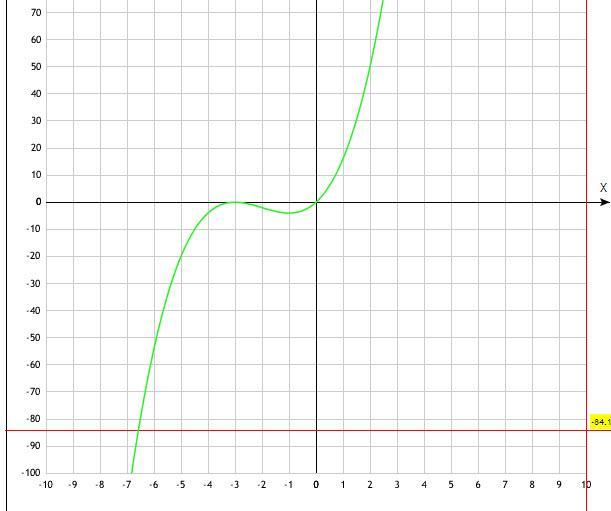
Найдите разность между наибольшим и наименьшим значениями функции y=x³+6x²+9x на отрезке (-3;0)​​

Answer 1

Найдем производную , потом  критические точки, выберем те из них, которые содержатся на указанном отрезке и найдем значения в этих точках и на концах отрезка, из которых найдем наибольшее и наименьшее, а потом из разность.

у'=(x³+6x²+9x)'=3x²+12x+9=3*(x²+4x+3); 3*(x²+4x+3)=0, по теореме, обратной теореме Виета, корни уравнения -3 и -1, оба входят в рассматриваемый отрезок.

у(-3)=(-3)³+6*(-3)²+9*(-3)=-27+54-27=0  наибольшее значение

у(-1)=(-)³+6*(-1)²+9*(-1) =-1+6-9=-4 наименьшее значение

у(0)=0 наибольшее значение

0-(-4)=4