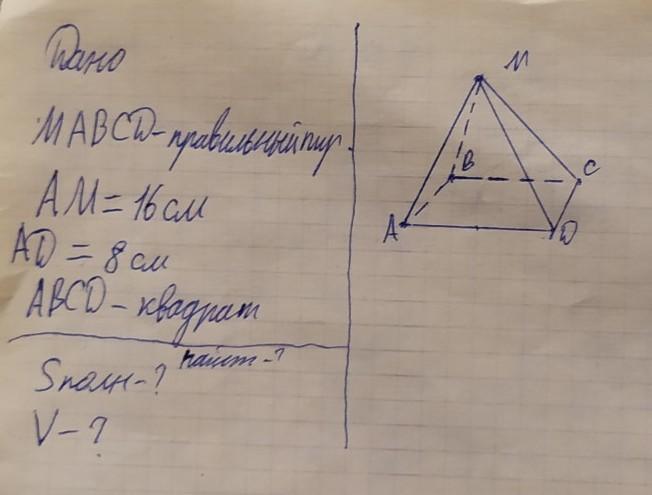
нужно решить задачу по геоометрии
Ответы
Ответ: Sполн = 64(√15 + 1) см²; V = (256√14)/3 см³
Объяснение:
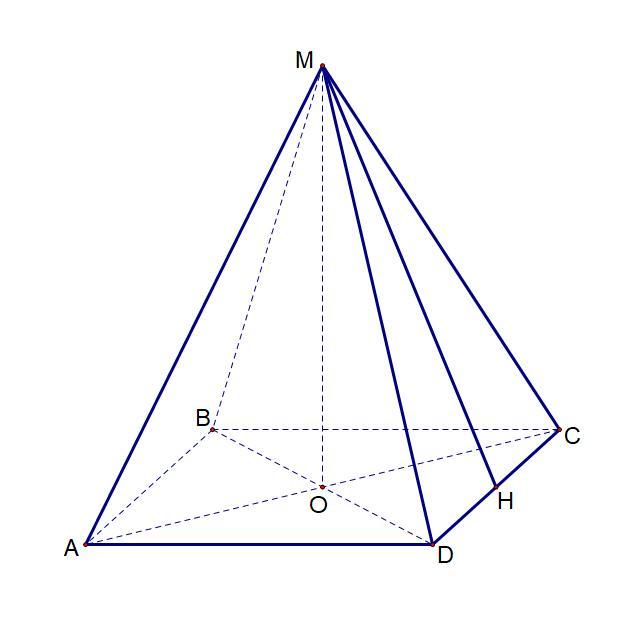
1. ΔMAD = ΔMCD = ΔMBC = ΔMAB (прав. пир.) ⇒ Sполн = 4*SΔmcd + Sосн
MD = MC (правильная пирамида) ⇒ ΔMCD - равнобедренный
Проведём MH⊥DC, DH = HC (ΔMCD - р/б)
DH = HC ⇒ DH = DC/2 = 8/2 = 4 см
Из ΔMHD по теореме Пифагора MH = √(MD² - DH²) = √(16² - 4²) =
= √(16(16-1)) = √16√15 = 4√15 см
Sосн = AD² = 8² = 64 см²
SΔmcd = 1/2 * CD * MH = 1/2 * 8 * 4√15 = 16√15 см²
Sполн = 4*16√15 + 64 = 64√15 + 64 = 64(√15 + 1) см²
2. Проведём высоту пирамиды MO. Так как пирамида правильная, то точка O -- пересечение диагоналей квадрата ABCD.
Vпир = 1/3 * Sосн * MO
Из ΔABD по теореме Пифагора BD = √(64 + 64) = √(64(1+1)) = √64√2 =
= 8√2 см
BO = OD (квадрат) ⇒ OD = BD/2 = 4√2 см
Из ΔMOD по теореме Пифагора MO = √(MD² - OD²) = √(16² - (4√2)²) =
= √(16² - 16*2) = √(16(16-2)) = 4√14 см
Vпир = 1/3 * Sосн * MO = 1/3 * 64 * 4√14 = (256√14)/3 см³