Предмет: Алгебра,
автор: xFuuuuuuuury
Помогите ребята, спасайте!! Много баллов!
Нужно найти область сходимости степенного ряда, помогите пожалуйста
Приложения:
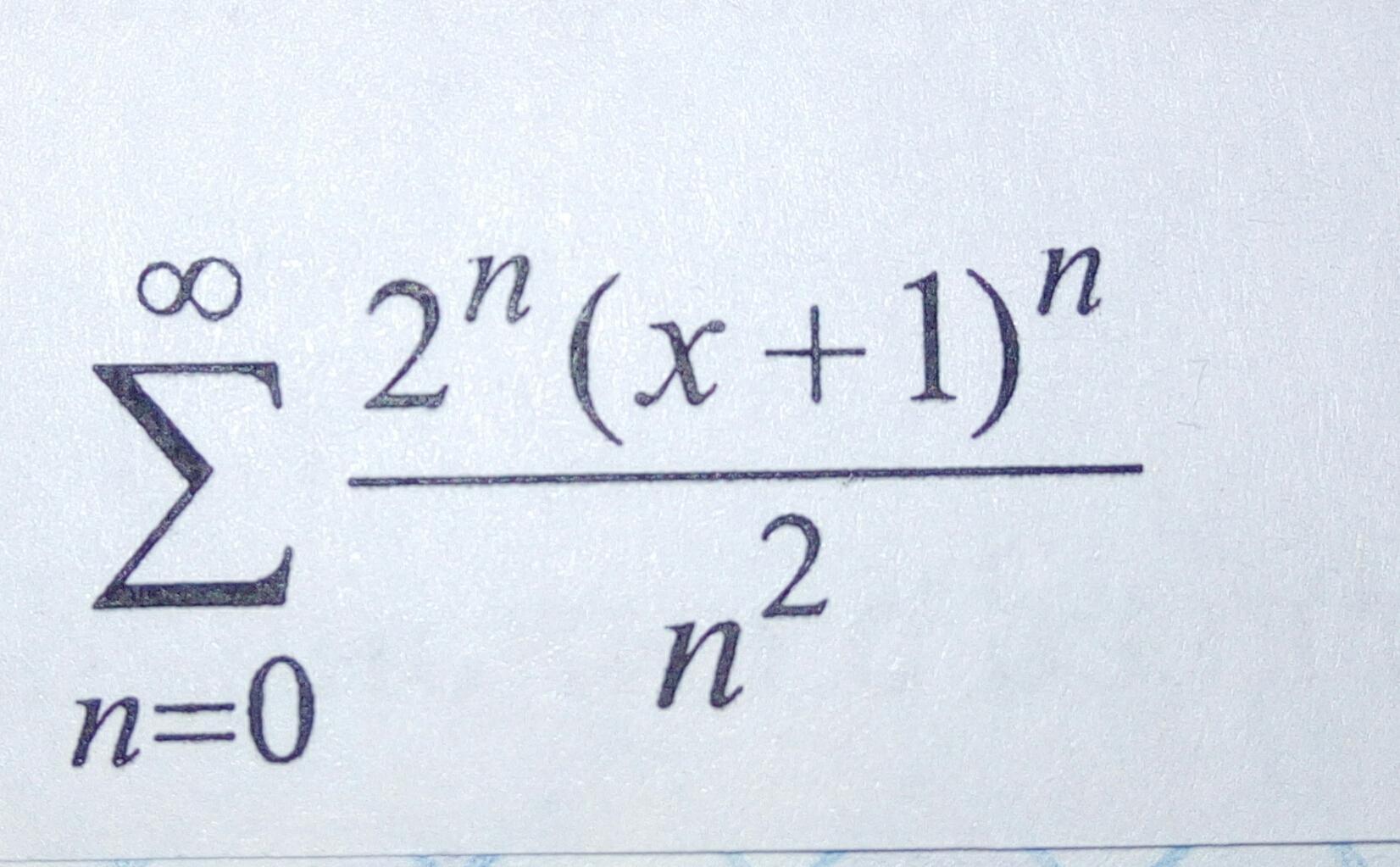
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Қазақ тiлi,
автор: asdanilrus4612
Предмет: География,
автор: Ilsurhi8370
Предмет: Математика,
автор: hairzhanova1767
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Полинария675