Предмет: Математика,
автор: dashababanina20
Вычислите определенный интеграл ,используя подходящую подстановку
Приложения:
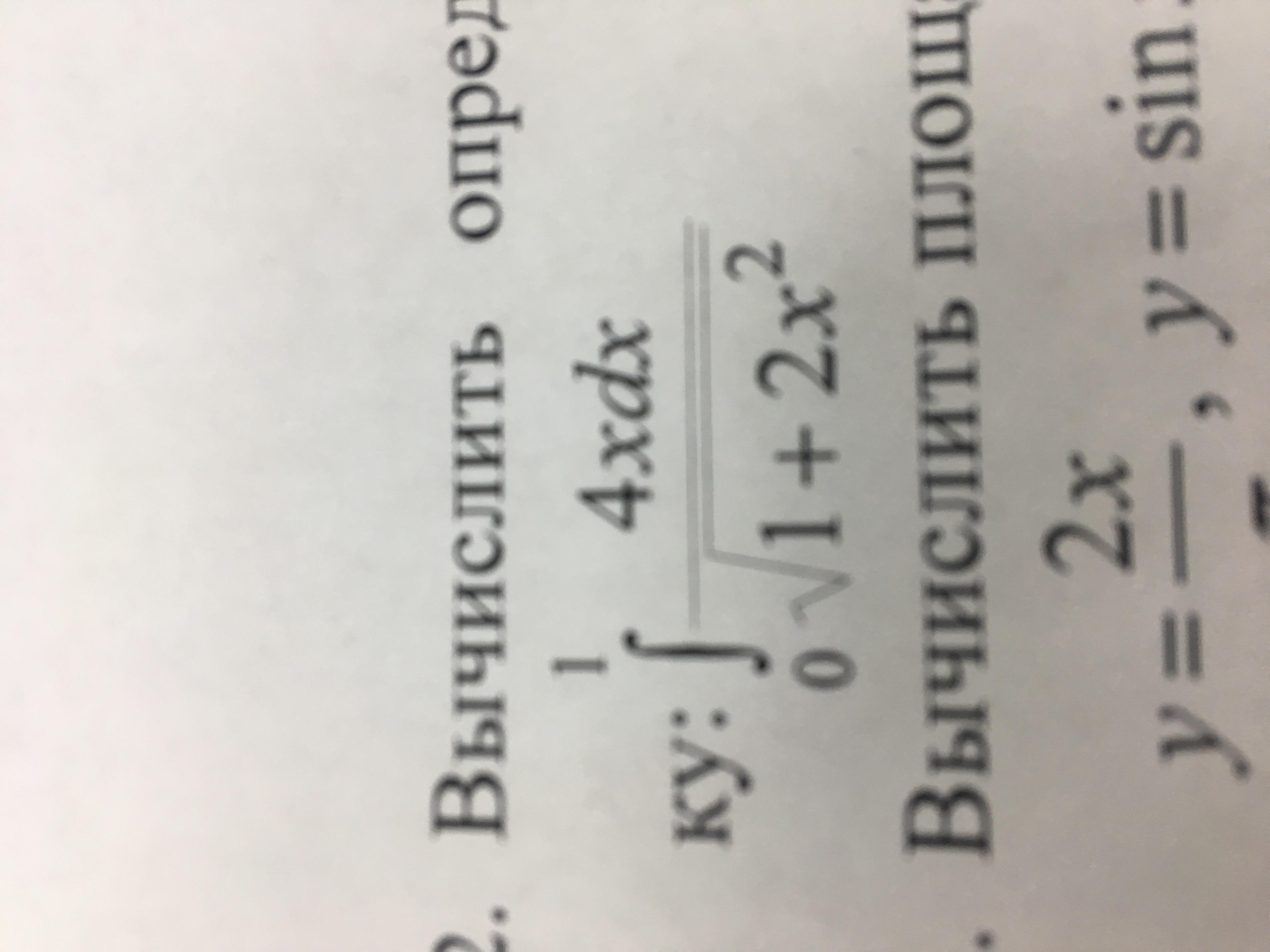
Ответы
Автор ответа:
0
Автор ответа:
0
Пусть 1+2х²=у, тогда d(1+2х²)=4xdx=dy; и интеграл примет вид ∫dy/√y=2√у
пределы интегрирования по у будут такими ув.=1+2=3; ун.=1+0=1
Берем теперь определенный интеграл от 1 до 3 для функции 1/√у, применяя формулу Ньютона - Лейбница, получим 2*√3-2*√1=2*(√3-1)
Похожие вопросы
Предмет: Биология,
автор: noname0090
Предмет: Математика,
автор: sofiahodakivska978
Предмет: Английский язык,
автор: vika8175tyty
Предмет: Литература,
автор: аля1210