Предмет: Математика,
автор: antonella
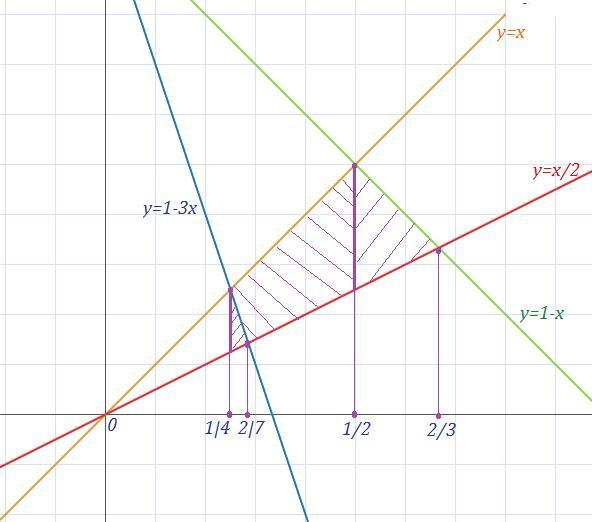
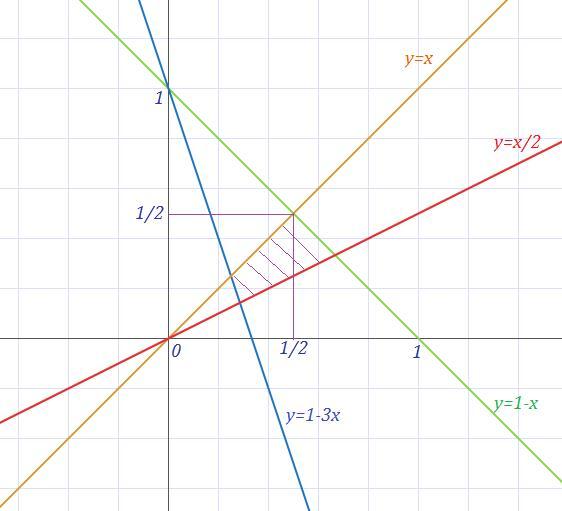
найти площадь фигуры ограниченной линиями y+x=1;y+3x=1;x=y;x=2y
Ответы
Автор ответа:
1
Приложения:
Похожие вопросы
Предмет: Физика,
автор: ArtemHyda
Предмет: ОБЖ,
автор: volohelizaveta
Предмет: Геометрия,
автор: enotik85874
Предмет: Литература,
автор: лиа3
Предмет: Алгебра,
автор: Лера1245111