Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!! Постройте график функции x|x|+|x|-5x. Определите при каких значениях m прямая y=m имеет с графиком ровно две общие точки. Очень нужно!!!! Заранее спасибо.

Answer 1

$y=x\cdot \begin{vmatrix}x\end{vmatrix}+\begin{vmatrix}x\end{vmatrix}-5x\\\\\begin{bmatrix}\begin{Bmatrix}x\ge 0\\y=x^2-4x\end{matrix}\\\begin{Bmatrix}x<0\\y=-x^2-6x\end{matrix}\end{matrix}$

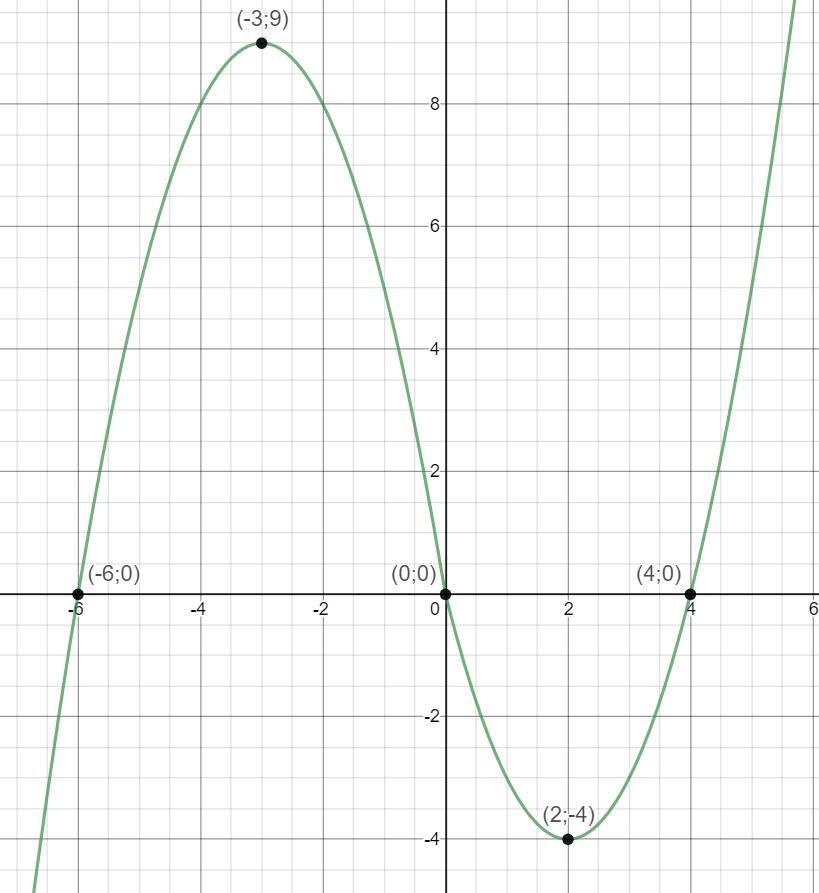
В первой системе есть парабола ветви которой направлены вверх, найдём координату вершины, нули функции, а так же ординату границы.

$y=x^2-4x=(x-2)^2-4,\;(2;-4)\\y=x(x-4),(0;0),(4;0)\\y(0)=0,(0;0)$

Построим эту параболу по трём точкам (вершина и нули) и сразу учтём ограничение.

Во второй системе есть парабола ветви которой направлены вниз, найдём координату вершины, нули функции  и ординату границы.

$y=-x^2-6x=-(x+3)^2+9,(-3;9)\\y=-x(x+6),(0;0),(-6;0)\\y(0)=0,(0;0)$

Построим эту параболу по трём точкам (вершина и нули) и сразу учтём ограничение, кстати точки в границах совпали, поэтому функция получиться непрерывной.

Смотри вниз.

Прямая y=m параллельна или совпадает с ось Ох, поэтому она будет иметь ровно две общий точки с графиком функции, когда будет касаться одной из парабол в её вершине, то есть в точках (-3;9) и (2;-4)

Значит m={-4;9}.

Ответ: m={-4;9}.