Question

Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания по углом 30'. (30' - 30 градусов).

Обязательно:

1) Полное решение, с объяснением.

2) Рисунок.

Answer 1

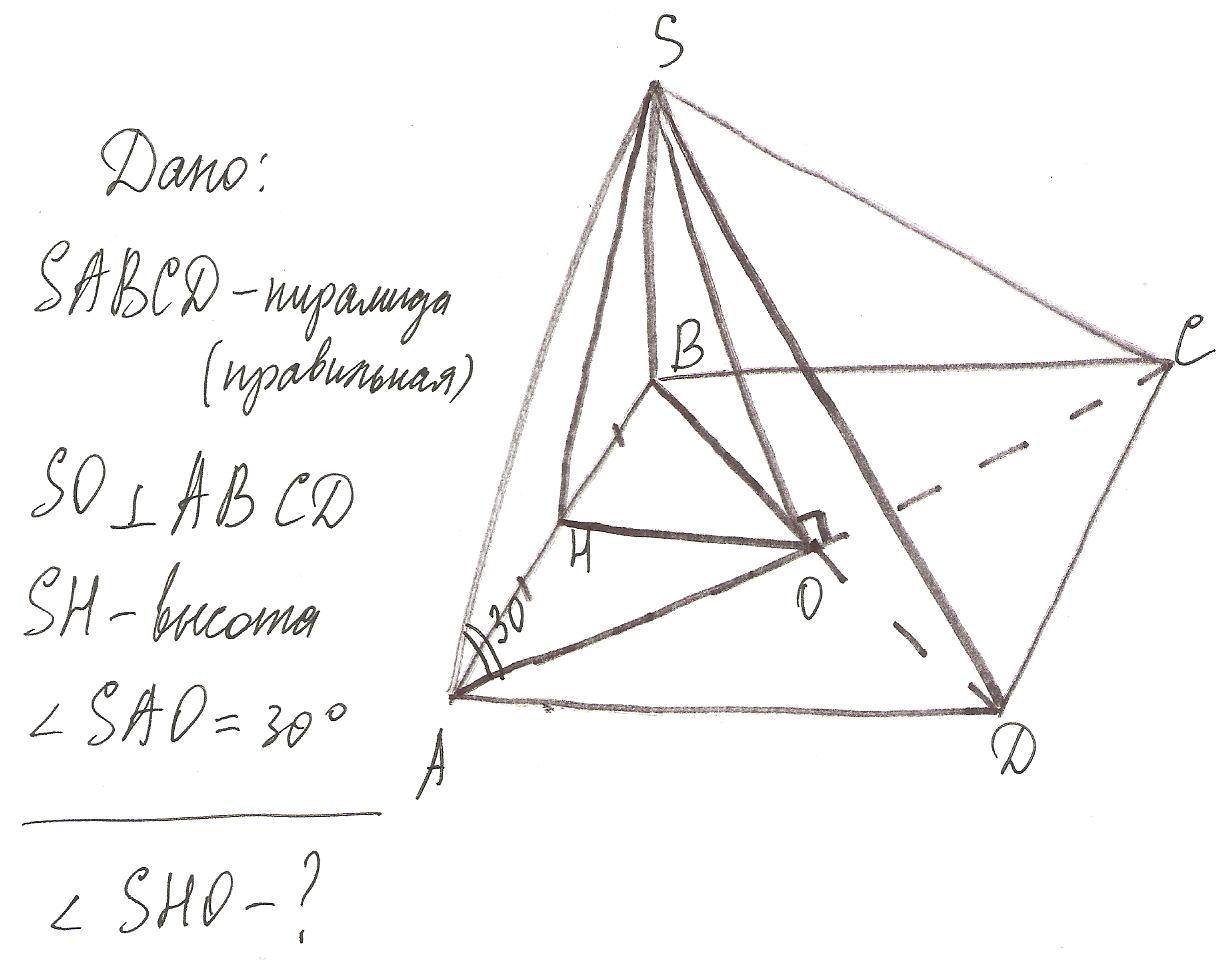
Дано:
на картинке

Решение:
Так как пирамида правильная и SO перпендикулярно ABCD, то SOA - прямоугольный треугольник. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов равен половине гипотенузы. Значит SO=SA/2.

Обозначим SA=2a, тогда SO=a. По теореме Пифагора найдем ОА:
$OA= sqrt{SA^2-SO^2}= sqrt{(2a)^2-a^2}= a sqrt{3}$

Так как в основании лежат квадрат, то он имеет равные взаимно перпендикулярные диагонали, которые точкой пересечений делятся пополам. Значит, треугольник АВО - прямоугольный и АО=ВО.
По теореме Пифагора находит АВ из прямоугольного треугольника АВО:
$AB= sqrt{AO^2+BO^2}= sqrt{(a sqrt{3} )^2+(a sqrt{3} )^2}= asqrt{6}$

Так как точка Н - середина АВ, то НВ=НА=АВ/2
Из прямоугольного треугольника OНВ находим OН по теореме Пифагора:
$OH= sqrt{BO^2-HB^2} = sqrt{AO^2-HB^2} = \ =sqrt{(a sqrt{3}) ^2-( frac{a sqrt{6} }{2})^2} =asqrt{( sqrt{3}) ^2-( frac{ sqrt{6} }{2})^2} =asqrt{3- frac{6 }{4}} =asqrt{ frac{6 }{4}} = frac{a sqrt{6} }{2}$

Из прямоугольного треугольника SOH:
$tgSOH= frac{SO}{OH} =a: frac{a sqrt{6} }{2} = frac{2}{ sqrt{6} } =frac{2cdot sqrt{6}}{ sqrt{6}cdot sqrt{6} } =frac{2sqrt{6}}{6 } =frac{sqrt{6}}{3 } \ Rightarrow SOH=mathrm{arctg} frac{sqrt{6}}{3 }$

Ответ: $mathrm{arctg} frac{sqrt{6}}{3 }$

Answer 2

посмотрите в приложении