как делать такое? подробно
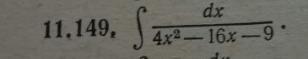
Ответы
Этот интеграл надо подогнать под табличный, а именно
∫du/(u²- a²)=(1/(2a))*㏑I(u-a)/(u+a)I+c
Вынесем за знак интеграла 1/4 и выделим в знаменателе квадрат разности по формуле а²-2ав+в²=(а-в)², затем введем замену у=(х-2), и воспользуемся тем, что d(x-2)=dx.
∫dx/(4x²-16x-9)=(1/4)∫dx/((x²-4x+4)-4-9/4)=(1/4)∫dx/((x-2)²-25/4)=
(1/4)∫d(x-2)/((x-2)²-25/4)={ введем замену u=x-2}=(1/4)∫du/(u²-(5/2)²)=
{применяем формулу ∫du/(u²-a²)=(1/(2a))*㏑I(u-a)/(u+a)I+c, в качестве а=5/2}=(1/4)*(1/(2*(5/2))*㏑I(u-a)/(u+a)I+c={подставляем вместо u (х-2)}=
(1/20)*㏑I(x-2-5/2)/(x-2+5/2)I+c=(1/20)*㏑I(2x-4-5)/(2x-4+5)I
+c=(1/20)*㏑I(2x-9)/(2x+1)I+c
Проверка.
((1/20)*㏑I(2x-9)/(2x+1)I+c)'=(1/20)*((2х+1)/(2х-9))*((2*(2х+1)-2*(2х-9))/(2х+1)²=
(1/10)*((2х+1)/(2х-9))*(((2х+1)-(2х-9))/(2х+1)²=
(1/10)*((2х+1)/(2х-9))*(((2х+1-2х+9))/(2х+1)²=(1/10)/(2х-9))*(10))/(2х+1)=
1/(4х²+2х-18х-9)=1/(4х²-16х-9) - получили подынтегральную функцию, решение выполнено верно.
Ответ (1/20)*㏑I(2x-9)/(2x+1)I+c