Предмет: Алгебра,
автор: valovvov
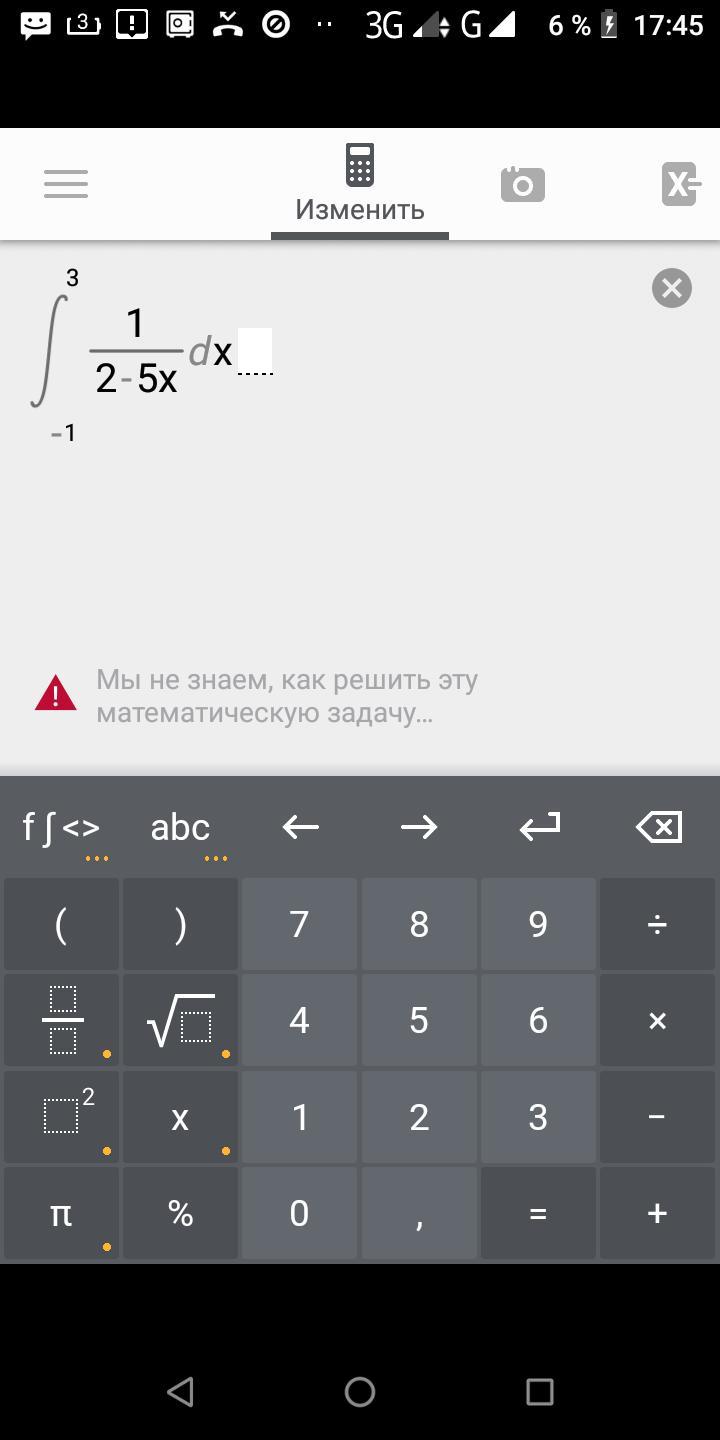
Решите интегралл: иньегралл от -1 до 3 (dx)/(2-5x) это дробь если что.
Заранее спасибо. Там на фото вместо 1 должно быть dx а в конце его не нет
Приложения:
Ответы
Автор ответа:
1
Интеграл расходится.
valovvov:
Спасибо огромное
Спасибо ещё раз
Похожие вопросы
Предмет: Литература,
автор: maksikmurko1
Предмет: Английский язык,
автор: kaliyeva0421
Предмет: Русский язык,
автор: uldanazhumanova28
Предмет: История,
автор: данил36н
Предмет: Математика,
автор: 171Лиза171