Предмет: Алгебра,
автор: lairysy

Сократить уравнения
Очень нужно, пожалуйста, помогите мне
Ответы
Автор ответа:
1
либо ты ошибся в написании, либо здесь действительно такой ответ..
lairysy:
У меня тоже так. Думаю что учительница сделала ошибку
нет , марьванна не виновата , знаменатель можно упростить
Автор ответа:
0
Ответ:
Объяснение: Решение : ///////////////////////////
Приложения:
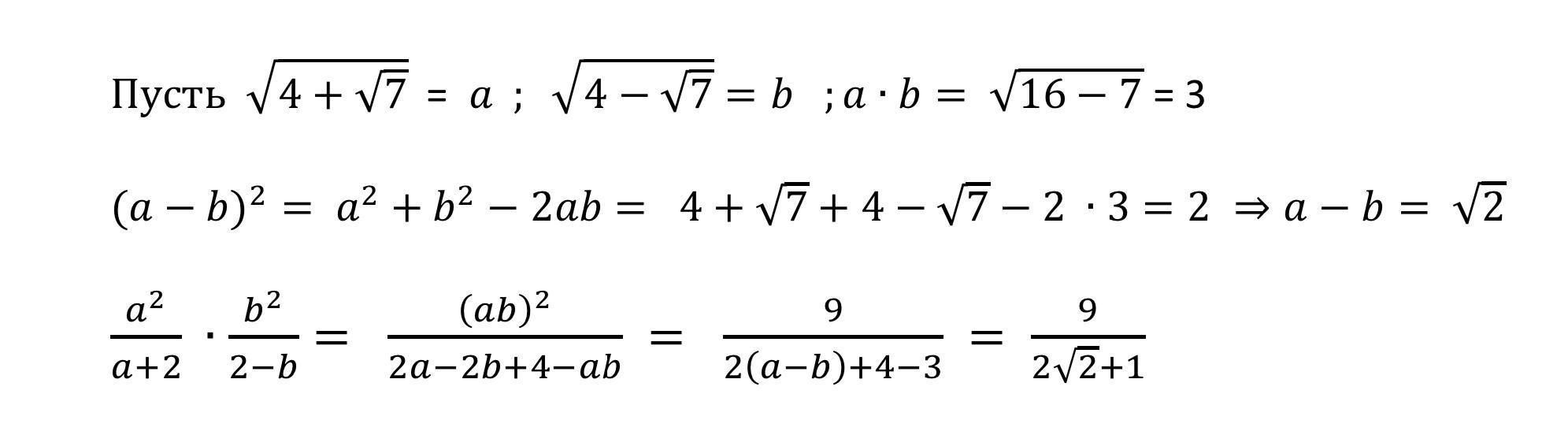
можно было использовать формулу сложного радикала , но уж больно она громоздкая и еще если домножить подкоренное выражение на 2 , то корень извлечется
Похожие вопросы
Предмет: Обществознание,
автор: saikorro
Предмет: Геометрия,
автор: ppomogii
Предмет: Алгебра,
автор: dwws21
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: kohanovskaa2