Предмет: Математика,
автор: serega54321
Помогите решить данные примеры:
1) Найти производную функции ![f(x)=\frac{1}{\sqrt[2]{x^{3} } } f(x)=\frac{1}{\sqrt[2]{x^{3} } }](https://tex.z-dn.net/?f=f%28x%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%5B2%5D%7Bx%5E%7B3%7D+%7D+%7D)
2) Взять определённый интеграл ![\int\limits^1_0 3{\sqrt[3]{x^{2} } } \, dx \int\limits^1_0 3{\sqrt[3]{x^{2} } } \, dx](https://tex.z-dn.net/?f=%5Cint%5Climits%5E1_0+3%7B%5Csqrt%5B3%5D%7Bx%5E%7B2%7D+%7D+%7D+%5C%2C+dx)
3) Найти производную сложной функции 
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
вот
Приложения:
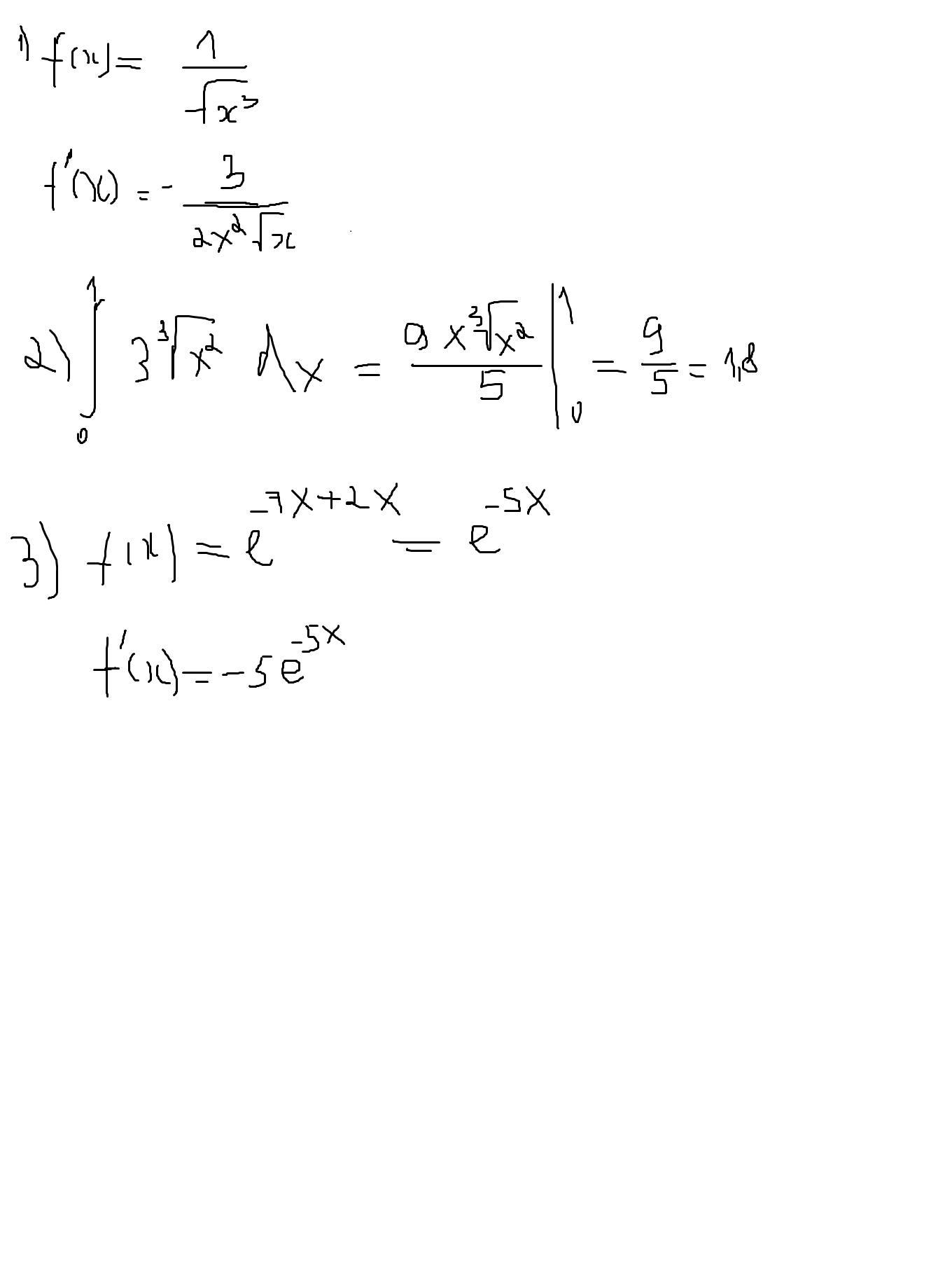
Автор ответа:
0
1. f'(x)=(1/√x³)'=(x^(-3/2))'=-1.5*x⁻⁵/²=-3/(2x²√x)
2. Сначала неопределенный интеграл,
∫3*(x^(2/3))dx=(3*x²/³⁺¹)/(2/3+1)=(9*x⁵/³)/5; теперь по формуле Ньютона -Лейбница возьмем определенный интеграл, подставив нижний и верхний пределы интегрирования. В нижнем ноль, в верхнем 9/5
Значит, 9/5-0=1.8
3. f'(x)=(e⁻⁷ˣ⁺²ˣ)'=(e⁻⁵ˣ)'=-5*e⁻⁵ˣ
Похожие вопросы
Предмет: Українська література,
автор: FreeBigBalls
Предмет: Русский язык,
автор: shadowrazeIrequiem
Предмет: Математика,
автор: n9680073617
Предмет: Химия,
автор: millernastya63Настя