Question

В треугольнике ABC угол A равен 120° . Известно, что AB=6 , а биссектриса угла A равна 4 . Найдите длину стороны AC.

Answer 1

Ответ:

≈11,51 ед.

Объяснение:

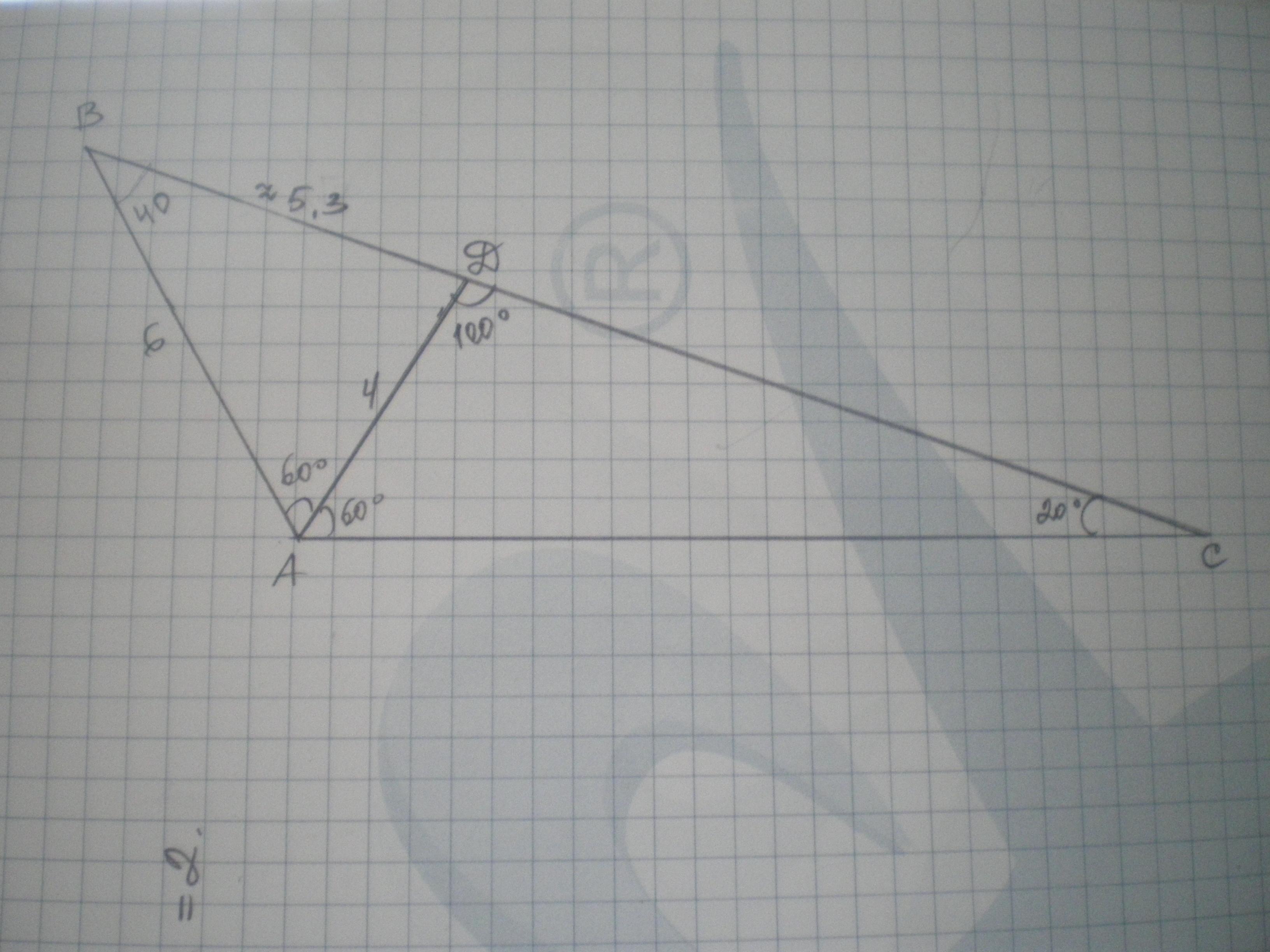
Дано: ΔАВС, ∠А=120°, АВ=6, АD - биссектриса, АD=4. Найти АС.

∠ВАD=∠DАС=120:2=60° по свойству биссектрисы.

По теореме косинусов

ВD²=АВ²+АD²-2*АВ*АD*cosВАD=36+16-48*1\2=28;  ВD=√28≈5,3 (ед.)

По теореме синусов

sinB=sin60*АD:ВD=0,5√3 * 4 : 5,3 = 0,6536;  ∠В=40°.

∠С=180-120-40=20°

∠АDС=180-60-20=100°

По теореме синусов АС=АD * sinАDС : sinC = 4*0,9848:0,3422≈11,51 (ед.)