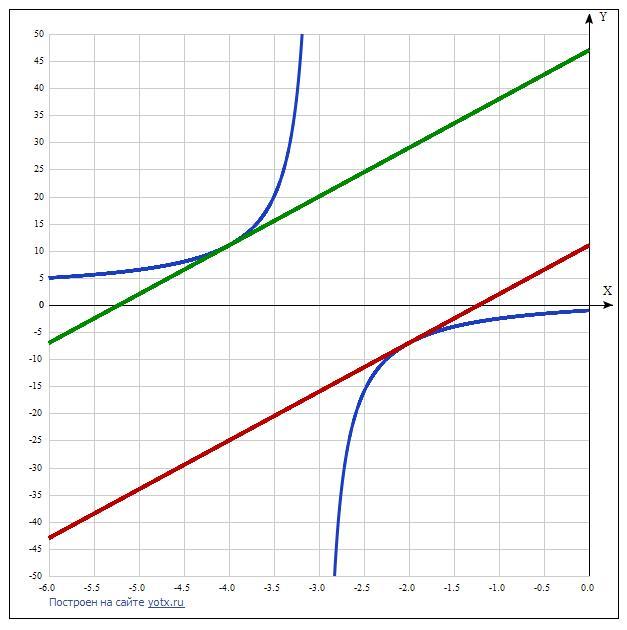
Если можно подробное решение

Ответы
Найдем координаты точек, в которых касательные к графику имеют угловой коэффициент угловой коэффициент = 9.
k = у' = [(2x - 3)/(x + 3)]' = [2*(x + 3) -1* (2x - 3)/(x - 3)² = 9 /(x + 3)².
Приравняем производную значению 9.
9 /(x + 3)² = 9, сократим на 9.
(x + 3)² = 1,
x + 3 = +-1.
Получаем 2 точки функции, в которых касательная имеет угловой коэффициент 9: х = 1 - 3 = -2 и х = -1 - 3 = -4.
Находим: y'(-2) = 9. y(-2) = -7.
y'(-4) = 9. y(-2) = 11
Запишем уравнения этих касательных:
1) y = 9 (x + 2) - 7 = 9x + 11.
2) y = 9 (x + 4) + 11 = 9x + 47.
Касательные пересекают ось абсцисс, значит, у = 0 Таким образом, если у = 0, то
1) у = 9x + 11 = 0, x = -11/9. Точка на оси Ох: ((-11/9); 0).
х = 0, y = 9*0 + 11 = 11. Точка на оси Оу: (0; 11).
2) у = 9x + 47 = 0, x = -47/9. Точка на оси Ох: ((-47/9); 0).
х = 0, y = 9*0 + 47 = 47. Точка на оси Оу: (0; 47).