Пожалуйста, решите и объясните свое решение МАКСИМАЛЬНО развернуто. Спасибо.
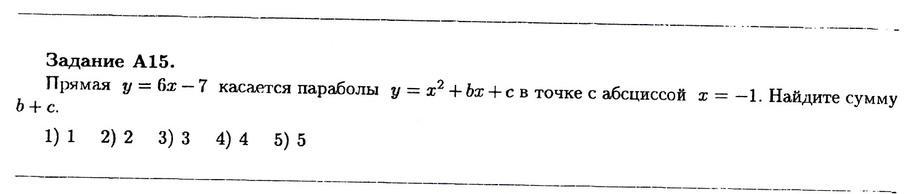
Ответы
Прямая у = 6х - 7 - касательная к параболе у = х² + bx + c в точке х = -1. Отсюда имеем: (х² + bx + c)' = 6; 2x + b = 6; 2·(-1) + b = 6; -2 + b = 6; b = 8.
Воспользуемся уравнением касательной: у = f '(x₀)(x - x₀) + f(x₀), где f '(x₀) = 6, x₀ = -1, f(x₀) = (-1)² - 8 + с = -7 + с.
Имеем: у = 6(x + 1) + с - 7 = 6х + 6 + с - 7 = 6х + с - 1.
По условию у = 6х - 7, отсюда с - 1 = -7; с = -6.
b + с = 8 - 6 = 2
Ответ: 2
у = 6х - 7 - касательная к параболе; геометрический смысл производной- это угловой коэффициент касательной, а он у нас есть. Это к=6. Общий вид уравнения касательной к графику, проходящему через точку с абсциссой x₀, такой у = f(x₀)+f '(x₀)(x - x₀) .
Найдем производную функции у'=(х² + bx + c)'=2x+ b; 2x+ b=6; У нас есть точка x₀=-1, подставим ее вместо х. Получим 2*(-1)+ b=6; откуда b=8.
В уравнении касательной у = f '(x₀)(x - x₀) + f(x₀),
f '(-1) = 6, f(-1) = (-1)² - 8 + с = -7 + с. Значит, у= -7+с+6*(х-(-1)); у=-7+с+6х+6; у=6х-1+с. Из условия у=6х-7, значит, -1+с=-7, откуда с=-6, а искомая сумма b+с=8-6=2.
Ответ: 2