Предмет: Математика,
автор: nurgul200274
Задание по математике.
Приложения:
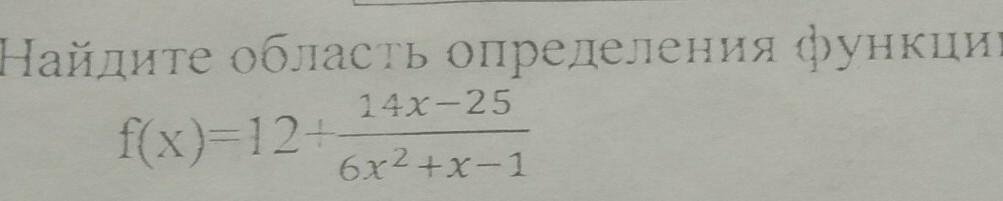
Ответы
Автор ответа:
2
Знаменатель не может равнять нулю, поэтому областью определения этой функции будет 6x²+x-1 ≠ 0, конечно можно привести всё к общему знаменателю, но наша задача не упростить выражение, а найти область определения.
Я решил уравнение равное нулю, поэтому при таких значениях х, исходное выражение будет равняться нулю, значит х должен не равняться этим значениям. Ответ можно записать двумя разными способами, но они означают совершенно одинаковые промежутки.
Или
Последнее означает все числа (действительные), кроме -0,5 и 1/3.
Приложения:

nurgul200274:
не могли бы вы мне написать на листке?
Вы не видите формулы? или вас интересует решение которое должно быть оформлено (без комментариев)
да меня интересует решение которое должно быть оформлено
сейчас приложу фото.
хорошо
спасибо
Похожие вопросы
Предмет: История,
автор: nonamehisdimandjek
Предмет: Биология,
автор: sgorbunova76
Предмет: Немецкий язык,
автор: Alisa1302
Предмет: Математика,
автор: Аноним