Question

Решить легкую стереометрическую задачку на 98 баллов.

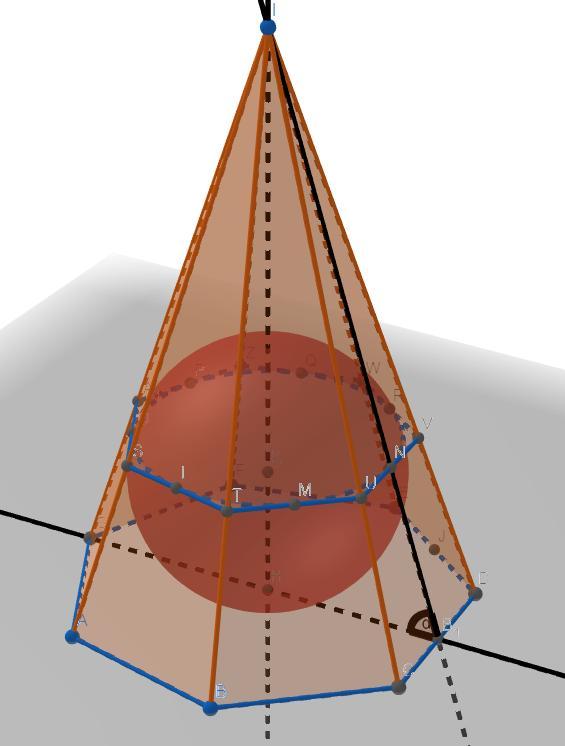
Доказать что отношение площади основания к площади полной поверхности у описанной пирамиды=

$\frac{S_o_s_n}{S_p_o_l_n}=\frac{cos(\alpha)}{1+cos(\alpha)}$

Где α- угол между боковой гранью и плоскостью основания

Answer 1

                       Доказательство:

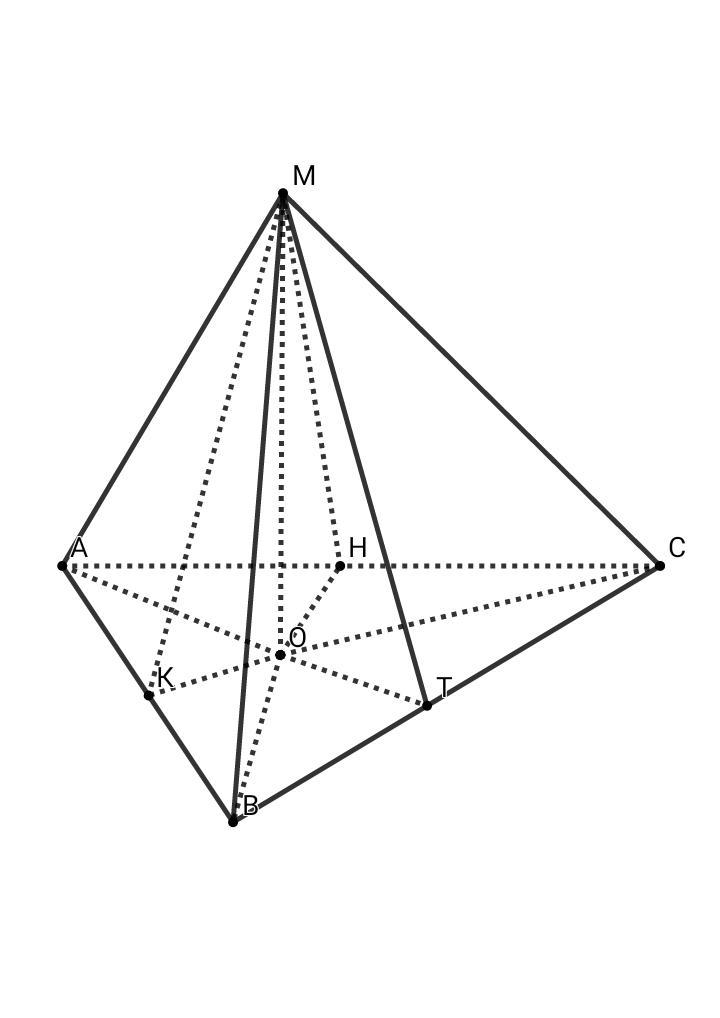
Если в пирамиду вписан шар, то вершина данной пирамиды проецируется в точку пересечения биссектрис основания, а боковые грани наклонены к основанию под одним и тем углом. Рассмотрим произвольную пирамиду MABC. Пусть r - радиус вписанной окружности в ΔАВС, тогда ОК = ОТ = ОН = r

В ΔМОТ:  cosα = OT/MT ⇒ MT = r/cosα

S бок.пов. = (1/2) • P • h = p • MT = p•r/cosα

S осн. = р • r

$\frac{Sosn}{Spoln}=\frac{Sosn}{Sosn+Sbok}=\frac{p*r}{p*r+\frac{p*r}{cosa}}=\\\\=\frac{p*r}{\frac{p*r*(1+cosa)}{cosa}}=\frac{cosa}{1+cosa}$

Доказано

Answer 2

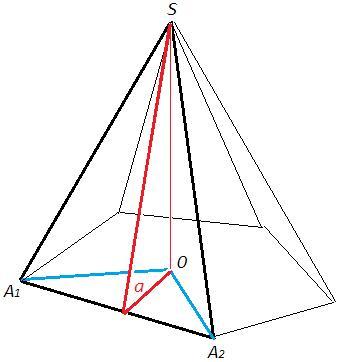
В пирамиду вписан шар - все боковые грани под углом a к плоскости основания.

O - основание перпендикуляра из вершины S.

S(A1OA2) = S(A1SA2) cosa (площадь ортогональной проекции)

Проекции боковых граней покрывают основание.

S осн = S(A1OA2) + S(A2OA3) + ...  

S бок = S(A1SA2) + S(A2SA3) + ...  

S осн /S бок = cosa

S полн /S осн = (S осн +S бок)/S осн = 1 + 1/cosa