Question

Найти площадь фигуры, ограниченной линиями параболой y=x^2+1 и прямой y=3-x

Answer 1

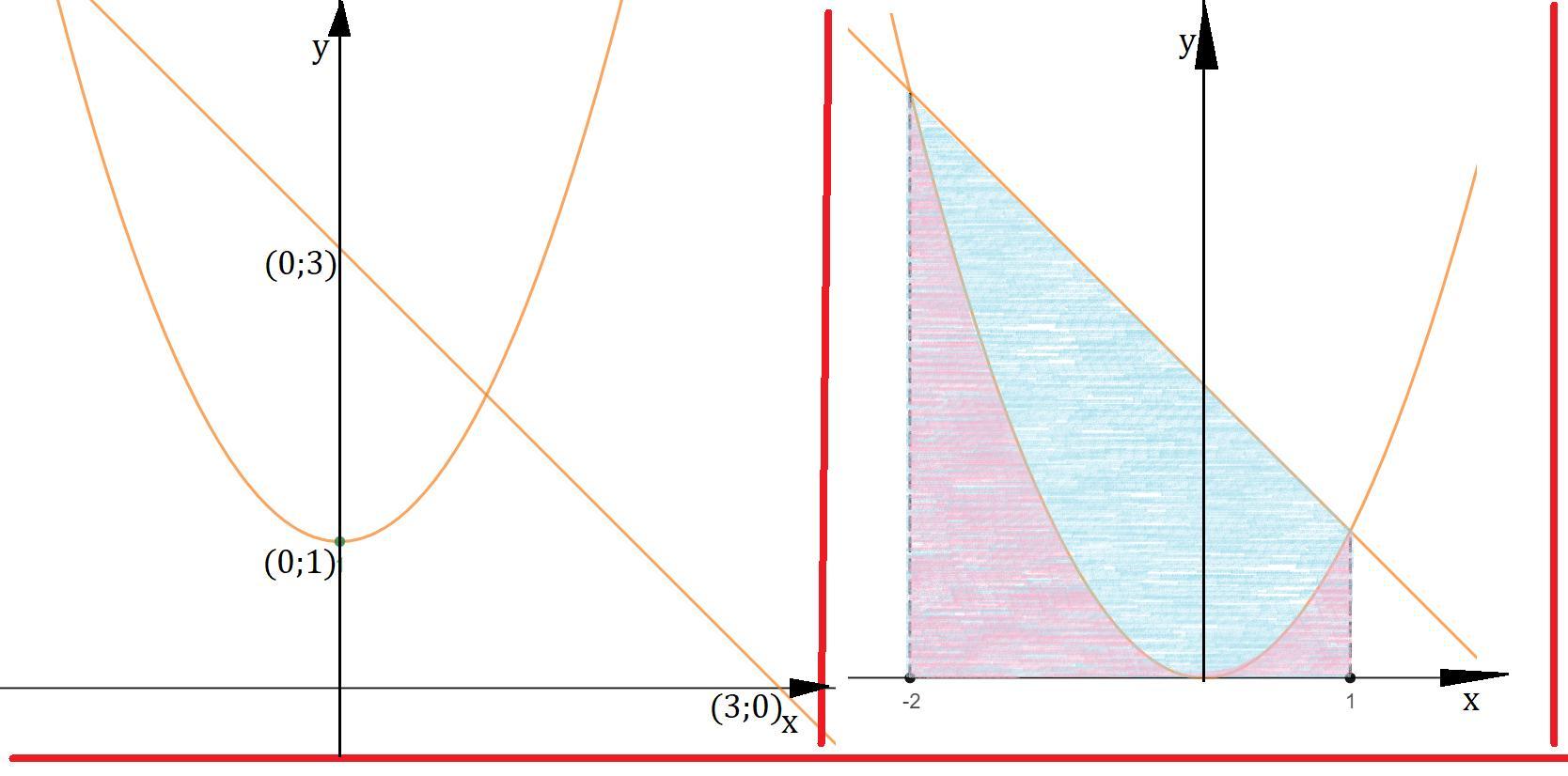
y=x²+1, это парабола ветви которой направлены вверх, а координаты вершины (0;1).

y=3-x, это прямая составляющая угол с ось абсцисс в 135° и поднята на 3 вверх.

Опустим каждый из эти графиков на 1, чтобы упростить себе задачу.

Получается y=x² и y=2-x, найдём абсциссы пересечений, чтобы определить промежуток интегрирования.

$x^2=2-x;\quad x^2+x-2=0;D=1+8=3^2\\x=\frac{-1\pm 3}{2}=\{-2;1\}$

Тогда площадь фигуры ограниченной этими линиями будет:

$S=\int\limits^1_{-2} {(2-x)} \, dx -\int\limits^1_{-2} {x^2} \, dx =\int\limits^1_{-2} {(2-x-x^2)} \, dx =\\(2x-\frac{x^2}{2}-\frac{x^3}{3})\begin{vmatrix}\\\end{matrix}^{1}_{-2}=(2\cdot 1-\frac{1^2}{2}-\frac{1^3}{3})-(2\cdot (-2)-\frac{(-2)^2}{2}-\frac{(-2)^3}{3})=\\\\(\frac{12-3-2}{6})-(\frac{-24-12+16}{6})=\frac{7+20}{6}=\frac{9}{2}=4,5.\\\\Otvet :4,5.$