Предмет: Геометрия,
автор: Nurzhan94
1) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, AC = 1. Найдите BH.
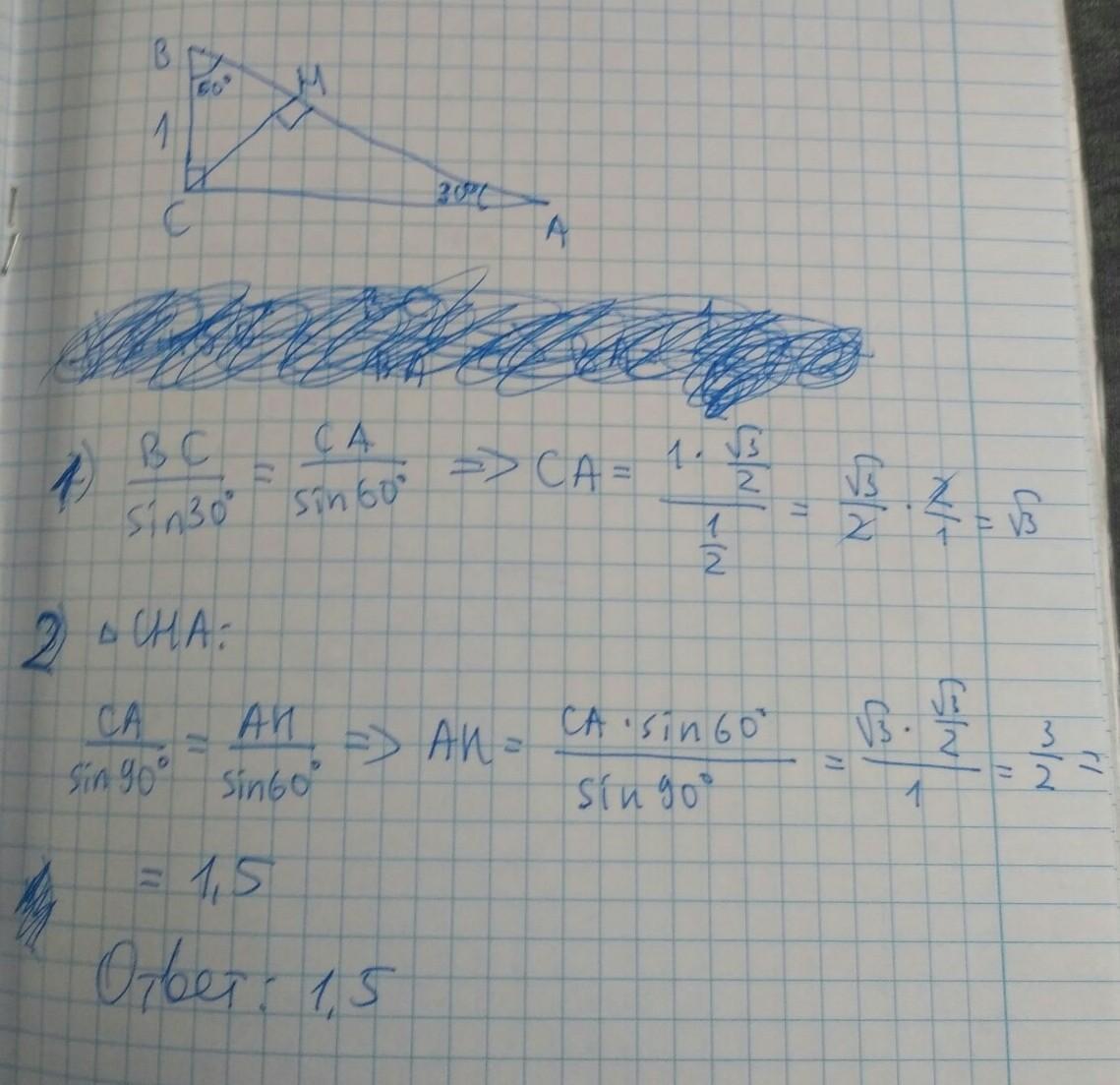
2) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, BC = 1. Найдите AH.
3) В треугольнике ABC угол C равен 90°, AC=4 sinA=3\5 Найдите высоту CH.
Ответы
Автор ответа:
8
1) в ΔАСН:
СН=0,5 (катет, лежащий против угла в 30° равен половине гипотенузы)
По теореме Пифагора:
АН² = АС² - СН² = 1 - 0,25 = 0,75
АН = √0,75 = 0,5 √3
в ΔАВС:
cos A = AC / AB
AB = 1 ÷ (√3 / 2) = 2√3 / 3
BH = AB - AH = 2√3 / 3 - 0,5√3 = (4√3 - 3√3) / 6 = √3 / 6
Ответ: √3 / 6
2) АВ = 2 ВС = 2 (катет, лежащий против угла в 30° равен половине гипотенузы)
∠В = 180° - ∠С - ∠А = 60°
cos B = BH / BC
BH = 1/2 × 1 = 1/2
AH = AB - BH = 2 - 1/2 = 1 1/2 = 1,5
Ответ: 1,5
3) sin A = CH / AC
CH = sin A × AC = 3/5 × 4 = 12/5 = 2,4
Ответ: 2,4
Автор ответа:
3
Решение в приложении. 1 фотка-1 номер; 2 фотка- 2 номер; 3 фотка- 3 номер.
Приложения:


Похожие вопросы
Предмет: Геометрия,
автор: 228lox228loxlox
Предмет: Математика,
автор: kewkader
Предмет: Физика,
автор: agritcuta2706544
Предмет: Математика,
автор: Леночка5111
Предмет: Математика,
автор: VeronikaZ05