Помогите, пожалуйста, ПОНЯТЬ, как это решить.
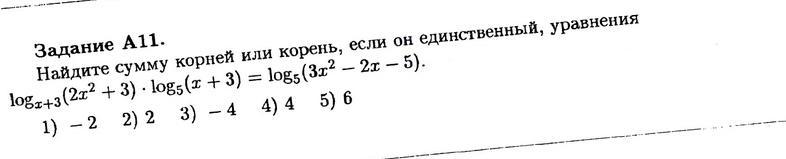
Ответы
Ответ:
Объяснение:
=====/////


㏒ₓ₊₃(2х²+3)*㏒₅(х+3) =㏒₅(3х²-2х-5)
ОДЗ уравнения. х+3>0; т.е. х>-3; х+3≠1, т.е. х≠-2; 2х²+3 всегда положительно, 3х²-2х-5>0; 3х²-2х-5=0; х₁,₂=(1±√(1+15))/3; х=5/3;х=-1 ; 3*(х-(5/3))(х+1)>0
решим это неравенство методом интервалов.
______-1______5/3___________
+ - +
Окончательно, область определения (-3;-2)∪(-2;-1)∪(5/3;+∞)
Перейдем к новому основанию в логарифме ㏒ₓ₊₃(2х²+3)=
㏒₅(2х²+3)/ ㏒₅(х+3) и упростим уравнение
((㏒₅(2х²+3))㏒₅(х+3))/ (㏒₅(х+3))=㏒₅(3х²-2х-5), после сокращения, а это можно делать, т.к. логарифм по основанию пять может быть равным нулю только при х=-2, но это число не входит в ОДЗ, получим
((㏒₅(2х²+3))=㏒₅(3х²-2х-5),⇒2х²+3=3х²-2х-5; х²-2х-8=0; по теореме, обратной теореме Виета, х=4; х=-2- лишний. Значит, у уравнения один корень х=4
Ответ 4. верный ответ 4)