Question

Помогите с этими заданиями!

Answer 1

7)

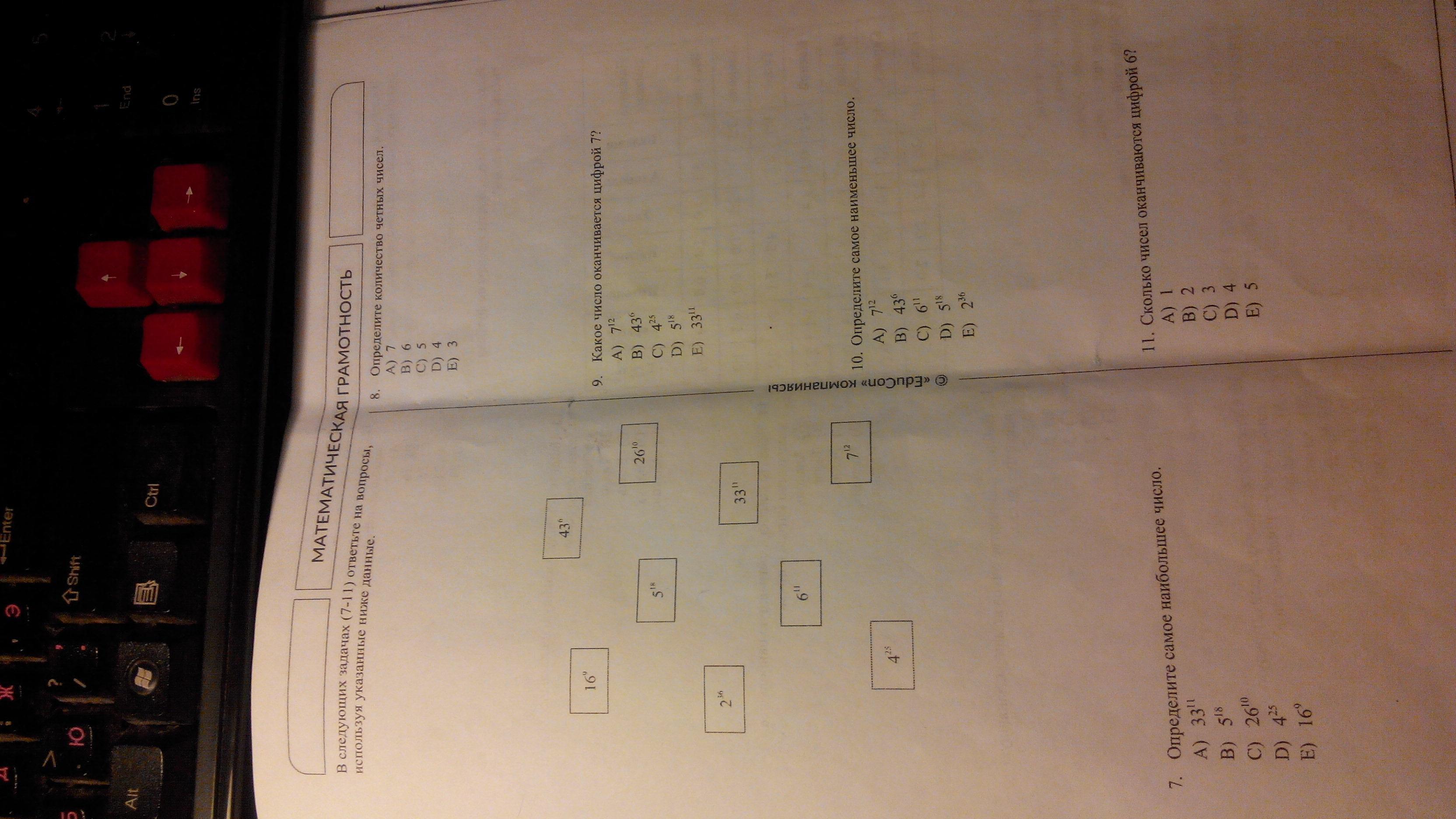
$33^{11};5^{18};26^{10};4^{25};16^9\\16^9=(4^2)^9=4^{18}<5^{18};5^{18}=(5^2)^9=25^9<26^{10}\\\\33^{11};26^{10};4^{25}\\26^{10}=2^{10}\cdot 13^{10}V4^{25}=(2^2)^25=2^{50};13^{10}V2^{40}\\13^{10}=(13^2)^5=\bold{169^5}<2^{40}=(2^8)^5=\bold{256^5}\\33^{11};4^{25}\\4^{25}=2^{50}=(2^5)^10=32^{10}<33^{11}\\\\Otvet :\;A)\;33^{11}.$

8)

нч - нечётно; ч - чётное.

Если нч · нч будет нч, поэтому нчⁿ=нч, где n - натуральное число.

Если ч · ч будет ч, поэтому чⁿ=ч, где n - натуральное число.

Таким образом: 43⁶ - нч; 16⁹ - ч; 26¹⁰ - ч; 5¹⁸ - нч; 2³⁶ - ч; 33¹¹ - нч; 6¹¹ - ч; 7¹² - нч; 4²⁵ - ч; всего 5 ч.

Ответ: С) 5.

9)

Для каждого числа в какой-то степени окончание равно или поздно начинают повторяться, окончание Х вообще зависит только от окончания чисел при перемножении которых получилось Х. Нижнем подчёркивание будем обозначать окончание.

7¹²: 7_7; 7²_9; 7³_3; 7⁴_1; 7⁵_7 - цикл 4, значит 7¹²_?=7⁸_?=7⁴_1

43⁶: 3_3; 3²_9; 3³_7; 3⁴_1; 3⁵_3 - цикл 4, значит 43⁶_?=43²_9

4²⁵ - ч, поэтому _7 не будет точно.

5¹⁸: 5ⁿ_5, где n - натуральное, поэтому _7 точно не будет.

33¹¹: для 3 цикл 4 (уже считали), поэтому 33¹¹_?=33⁷_?=33³_7

Ответ: E) 33¹¹.

10)

$7^{12};43^6;6^{11};5^{18};2^{36}\\7^{12}=(7^2)^6=49^6>43^6\\6^{11}=(6^2)^{5,5}=36^{5,5}<43^6\\6^{11};5^{18};2^{36}\\5^{18}=(5^4)^{4,5}=\bold{625^{4,5}}>2^{36}=(2^9)^4=\bold{512^4}\\6^{11};2^{36}\\6^{11}=(6^3)^{11/3}=\bold{216^{3\frac{2}{3}}}<2^{36}=(2^8)^{36/8}=\bold{256^{4,5}}\\\\Otvet :\;C)\;6^{11}.$

11)

Та же схема, что и в 9)

43⁶: в последовательности окончаний тройки нету цифры 6, поэтому точно не подходит.

16⁹: 6ⁿ_6, где n натурально, подходит.

26¹⁰: 6ⁿ_6, где n натурально, подходит.

5¹⁸: 5ⁿ_5, где n натурально, не подходит.

2³⁶: 2_2; 2²_4; 2³_8; 2⁴_6; 2⁵_2 - цикл 4, поэтому 2³⁶_?=2⁴_6, подходит.

33¹¹: в последовательности окончаний тройки нету цифры 6, поэтому точно не подходит.

6¹¹: 6ⁿ_6, где n натурально, подходит.

7¹²: в последовательности окончаний семи нету цифры 6, поэтому точно не подходит.

4²⁵: 4_4; 4²_6; 4³_4 - цикл 2, поэтому 4²⁵_?=4¹_4, не подходит.

Ответ: D) 4.