Предмет: Геометрия,
автор: ParkHaru
Ребят, снова нужна помощь
Помогите пожалуйста
(См. На фото)
Приложения:
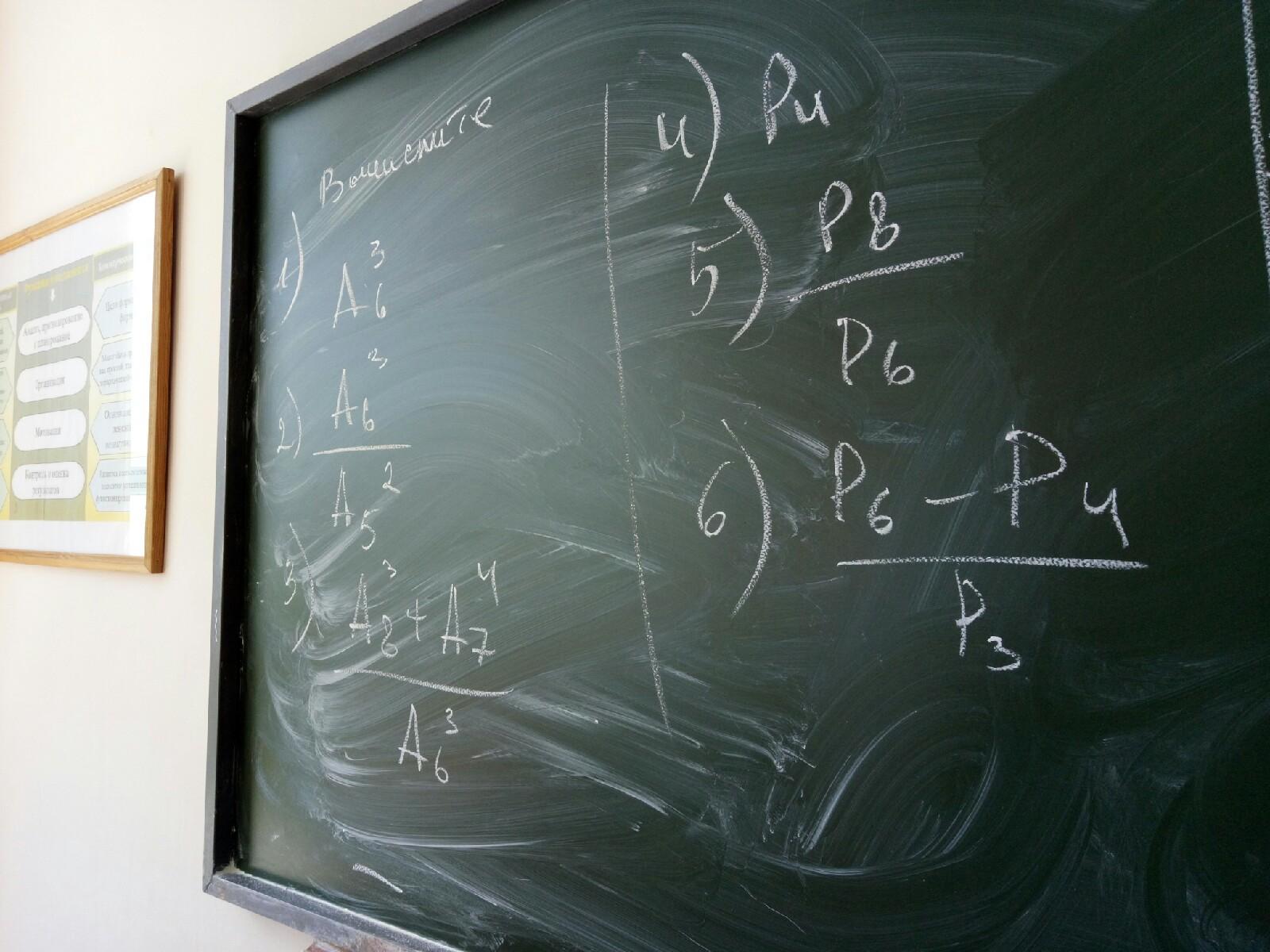
Ответы
Автор ответа:
0
Ответ:
Объяснение:
======/===
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: m5636454078
Предмет: Математика,
автор: kirillstepanchenko5
Предмет: Математика,
автор: kozjar201566
Предмет: Математика,
автор: ZZZZZSWISSZZZZZ
Предмет: Математика,
автор: ИринаZ