Предмет: Алгебра,
автор: nemoy99
Помогите решить уравнение с лимитом
Приложения:
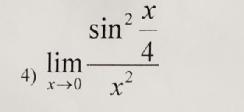
Ответы
Автор ответа:
3
= limₓ₋₀(sin(x/4))/x·limₓ₋₀(sin(x/4))/x = 0,25limₓ₋₀(sin(x/4))/(x/4)·0,25limₓ₋₀(sin(x/4))/(x/4) = 0,25·1·0,25·1 = 0,0625
Автор ответа:
1
используем 1-й замечательный предел
lim (x->0) sin (x) / x = 1
lim (x->0) sin² (x/4) / x² = lim (x->0)1/4 sin(x/4)/(x/4) * lim(x->0) 1/4 * sin(x/4) / (x/4) = 1/4 * 1/4 * lim (x->0) sin(x/4)/(x/4) * lim (x->0) sin(x/4)/(x/4) = 1/4*1/4*1*1 = 1/16
Похожие вопросы
Предмет: Математика,
автор: kapriz3084
Предмет: Физика,
автор: NightmareKiller
Предмет: Английский язык,
автор: maksimtelyatnik2010
Предмет: География,
автор: Monika4002
Предмет: Математика,
автор: Аноним