Найти пределы, не пользуясь правилом Лопиталя.
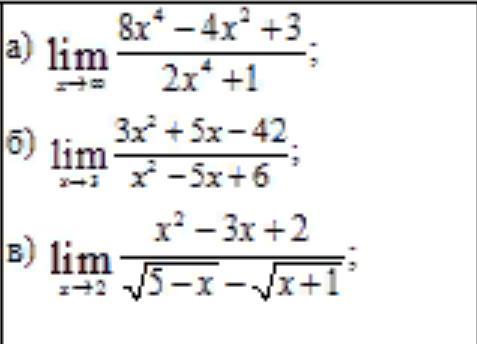
Ответы
а) Ответом на этот пример будет отношение коэффициентов при старших степенях переменной числителя и знаменателя, поскольку в числителе и знаменателе - стандартные многочлены 4-й степени и х стремится к ∞; 8/2=4
б)Разложим предварительно многочлены на линейные множители.
3х²+5х-42=0; х₁,₂=(-5±√(25+3*4*42) )/6=(-5±√529)/6=(-5±23)/6; х₁=3; х₂=-14/3; 3х²+5х-42=3*(х-3)(х+14/3)=(х-3)(3х+14); х²-5х+6=0, по теореме, обратной теореме Виета х₁=2; х₂=3; х²-5х+6=(х-2)(х-3). Разделим числитель на знаменатель, с учетом разложений.
(3х²+5х-42)/(х²-5х+6)=(х-3)(3х+14)/(х-2)(х-3)=(3х+14)(х-2). предел от (3х+14)(х-2) при х стремящемся к 3, равен (3*3+14)(3-2)=9+14=23
в) разложение числителя х²-3х+2 , предварительно с подсчитанными по теореме, обратной теореме Виета корнями уравнения х²-3х+2=0, х₁=1; х₂=2, примет вид х²-3х+2=(х-1)*(х-2). Домножим числитель и знаменатель на скобку (√(5-х)+√(х+1)), сопряженную знаменателю. В знаменателе вырисовалась разность квадратов (а-в)*(а+в)=а²-в², т.е. (5-х)-(х+1)=5-х-х-1=4-2х=-2*(х-2), а числитель примет вид
(√(5-х)+√(х+1))*(х-1)(х-2). После деления числителя на знаменатель получим
((√(5-х)+√(х+1))*(х-1)(х-2))/(-2*(х-2))=-((√(5-х)+√(х+1))*(х-1))/(2*(х-1)), подставим вместо х=2, получим -(√3+√3)(2-1)/(2*(2-1))=-2√3/2=-√3