Question

укажіть найбільше ціле значення параметра a при якому не має розвязків нерівність x^2-|2x-1| < a

Answer 1

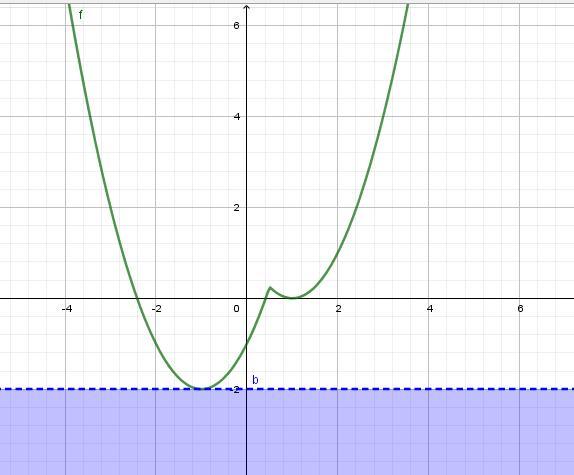
Построим график функции $y=x^2-|2x-1|=\displaystyle \left \{ {{x^2-2x+1,~~x\geq0.5} \atop {x^2+2x-1,~~~x <0.5}} \right.$

Если подставим a = -2, то $x^2-|2x-1|+2<0$

Если x ≥ 0.5, то $x^2-2x+1+2<0~~\Rightarrow~~ (x-1)^2+2<0$

Это неравенство не выполняется для x ∈ [0.5;+∞).

Если x < 0.5, то $x^2+2x-1+2<9~~~\Rightarrow~~~ (x+1)^2<0$

Это неравенство тоже неверно.

При y≤-2, т.е. при a≤-2 неравенство решений не имеет. Откуда наибольшее целое значение параметра: a = -2.