50 БАЛЛОВ!!!Срочно! Пожалуйста помогите!
В прямоугольной трапеции ABCD углы A и B прямые, а также BC=9, AD=25, CD=20. Найдите периметр трапеции, длину меньшей диагонали и расстояние от точки A до прямой CD.
периметр диагональ ρ(A;CD)
Ответы
Ответ:
Объяснение: 1)проведем высоту СН=АВ НД=25-9=16
из прямоуг.ΔСНД СН^2=20^2-16^2=144 CH=12=AB
периметр P=12+9+20+25=66
2)ΔABC-прямоуг. , АС^2=AB^2+BC^2=12^2+9^2=225 AC=15
3) ΔACD-прямоуг. так как 25^2=20^2+15^2→расстояние от точки A до прямой CD равно AC=15
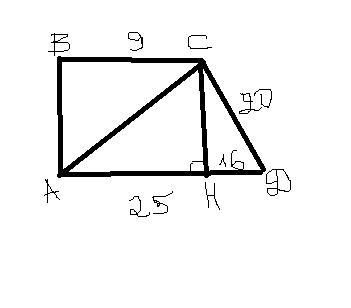
1.Пусть дана трапеция АВСД, чтобы найти периметр, НЕ ХВАТАЕТ только стороны АВ, которая равна высоте СТ, проведенной к стороне АД из вершины С. Точка Т лежит на АД, т.к. СТ⊥АД, то по теореме Пифагора из ΔСТД найдем СТ=√(20²-16²)=√(36*4)=12, значит периметр равен
АД+ВС+СД+АВ=25+9+20+12=66/см/
2.Большая диагональ лежит против тупого угла С, тогда меньшая диагональ АС, которую найдем из ΔАВС ;
АС=√(АВ²+ВС²)=√(12²+9²)=√(144+81)=15/см/
3.В треугольнике АСД стороны АС=15; СД=20; АД=25, и связаны между собой таким отношением -квадрат большей стороны равен сумме квадратов двух других, действительно, 25²=20²+15²,625=400+225, но тогда по теореме, обратной теореме Пифагора треугольник АСД - прямоугольный с прямым углом С, а раз так, То АС- расстояние от точки А до прямой СД, это расстояние ρ(A;CD) равно АС=15см