Предмет: Математика,
автор: sergei916
f(xy) = y/ x^2-y^2
помогите решить, буду благодарен.
нужно найти частные производные
Приложения:
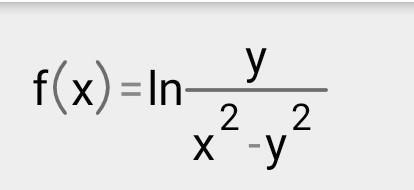
Ответы
Автор ответа:
1
Чтобы было легче взять производную по у воспользуемся свойствами логарифма
Похожие вопросы