Предмет: Алгебра,
автор: juliyasemyan
Решите неравенство:
(|x-1|+10)/(4|x-1|+3)>2
Ответы
Автор ответа:
2
Замена |x-1|=t, t>=0 тогда
--------(-3/4)++++++(4/7)--------->t
t>=0, поэтому t принадлежит [0;4/7)
х принадлежит (3/7;11/7)
ОТВЕТ: (3/7;11/7)
См. также приложение
Приложения:
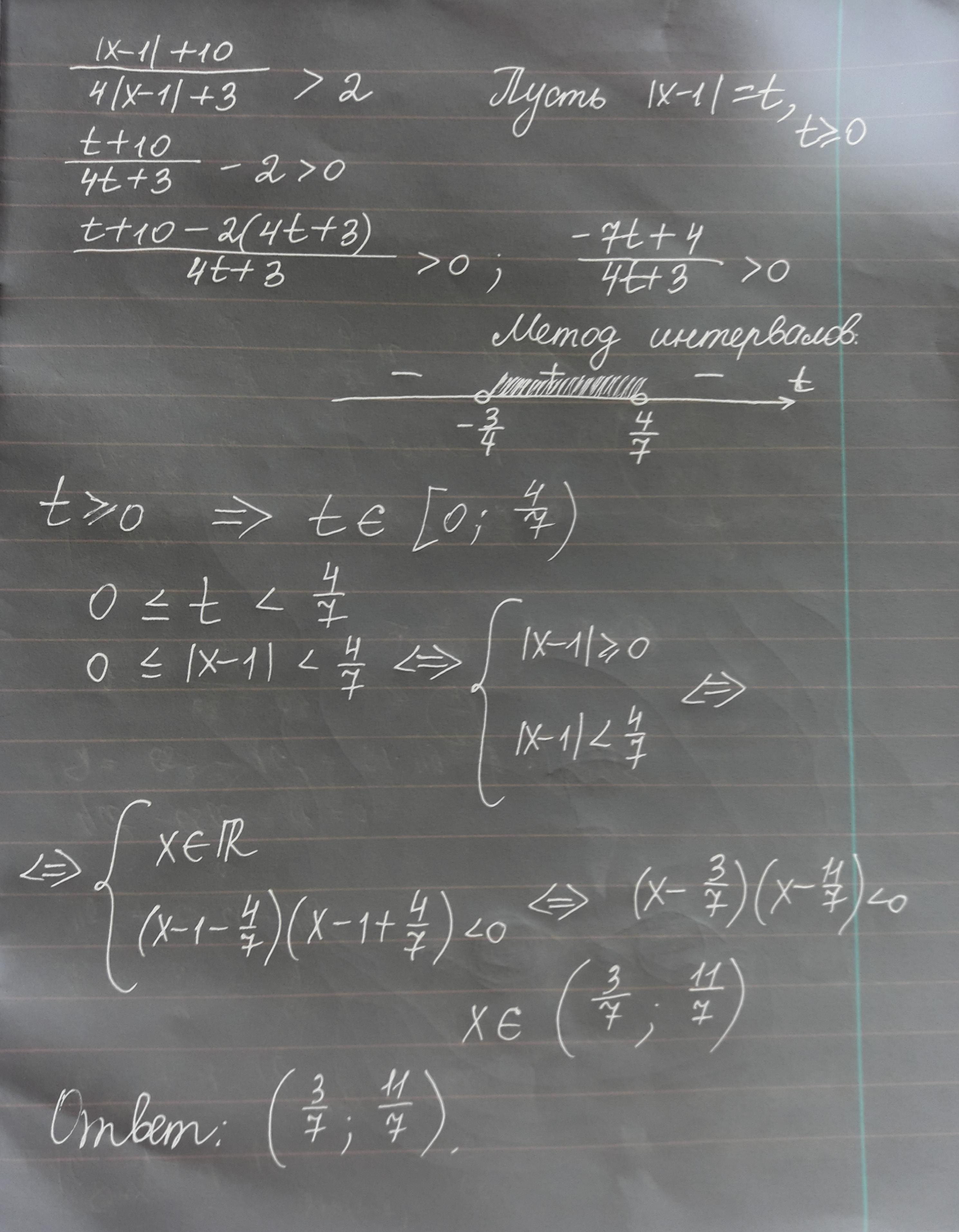
оо ура
Можешь, пожалуйста, подробнее написать как решить после (-7t+4)/(4t+3)>0
Методом интервалов. Знаешь?)
нет)
я не понимаю что происходит на месте второго троеточия
Через час всё подробно распишу
Чуваак
я поняла всё до момента (-7t+4)/(4t+3)>0
ниже метод интервалов, там числа -3/4 и 4/7
я понимаю что ты уже написал подробно (куда ещё подробней), но откуда они взялись?
Похожие вопросы
Предмет: Английский язык,
автор: standuser
Предмет: Английский язык,
автор: Znatbxochy
Предмет: История,
автор: 230709amorozov
Предмет: Физика,
автор: AntropovaValya01
Предмет: Математика,
автор: kseniazharko
(7t - 4)/(4t + 3)< 0