Предмет: Алгебра,
автор: helpme6770
Очень срочно надо все кто видит помооите
Приложения:
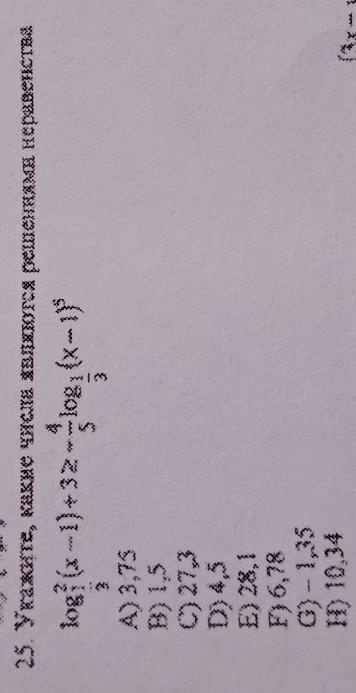
Ответы
Автор ответа:
0
Ответ: A) 3, 75.
Объяснение:
log²₁/₃(x-1)+3≥-(4/5)*log₁/₃(x-1)⁵
ОДЗ: x-1>0 x>1 x∈(1;+∞).
log²₁/₃(x-1)+(4/5)*log₁/₃(x-1)⁵+3≥0
log²₁/₃(x-1)+4*log₁/₃(x-1)+3≥0
Пусть log₁/₃(x-1)=t ⇒
t²+4t+3≥0
t²+4t+3=0 D=4 √D=2
t₁=log₁/₃(x-1)=-3 x-1=(1/3)⁻³ x-1=3³ x-1=27 x₁=28
t₂= log₁/₃(x-1)=-1 x-1=(1/3)⁻¹ x-1=3¹ x-1=3 x₂=4. ⇒
(x-4)(x-28)≥0
-∞__+__4__-__28__+__+∞
x∈(-∞;4]U[28;+∞)
Учитывая ОДЗ: x∈(1;4]U[28;+∞).
Похожие вопросы
Предмет: Геометрия,
автор: asbondini44
Предмет: История,
автор: dianaakmatova125
Предмет: Алгебра,
автор: veronia3003
Предмет: Алгебра,
автор: ингтн7е69ие
Предмет: Математика,
автор: муратхан4