Question

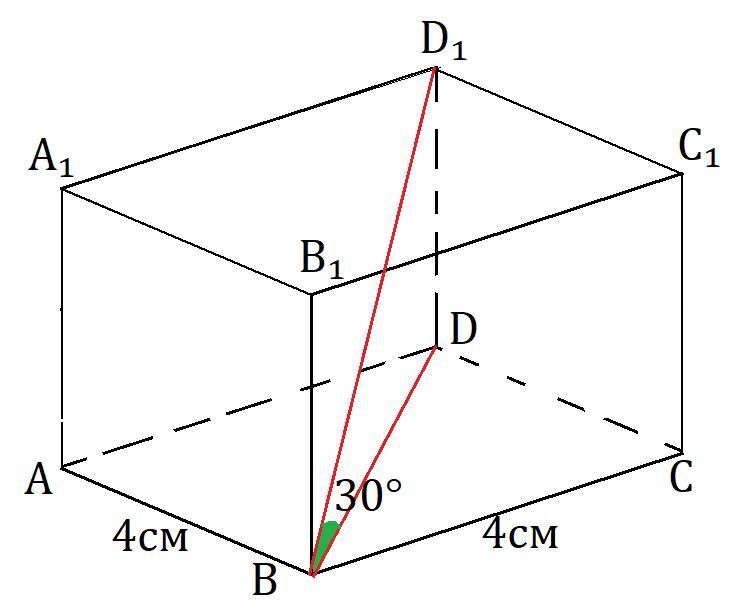
В правильной 4-х угольной призме, со стороной основания 4см, проведена диагональ призмы под углом 30 градусов к основанию. Найти объем(V)

Answer 1

Итак.

Призма правильная, поэтому в основаниях правильные четырёхугольники, то есть квадраты, а боковые рёбра перпендикулярны основанию призмы.

По условию ∠D₁BD = 30°; ∠D₁DB = 90° т.к.  DD₁ ⊥ (ABC).

Таким образом в прямоугольном ΔD₁BD: DD₁ = tg(D₁BD) · BD. BD=4√2 см как диагональ квадрата со стороной 4 см, поэтому DD₁ = 4√2 /√3  см

Объём правильной призмы можно найти через боковое ребро и площадь основания таким образом.

$V=DD_1\cdot S_{ABCD}=\frac{4\sqrt{2}cm}{\sqrt{3}}\cdot 16cm^2=\\\frac{64\sqrt{6}}{3}cm^3\\\\Otvet\!\!:\;\frac{64\sqrt{6}}{3}cm^3.$