Question

Где ошибки в 13 и 15?

Answer 1

13. В решении потерян второй корень.

$\cos(2x)+5\sqrt3\sin x+8=0\\1-2\sin^2x+5\sqrt3\sin x+8=0\\-2\sin^2x+5\sqrt3\sin x+9=0~~~|\cdot(-1)\\2\sin^2x-5\sqrt3\sin x-9=0$

Квадратное уравнение относительно переменной   sin x

$D=(5\sqrt3)^2-4\cdot2\cdot(-9)=75+72=147=(7\sqrt3)^2\\\\1)~\sin x=\dfrac{5\sqrt3-7\sqrt3}4=\dfrac{-2\sqrt3}4=-\dfrac{\sqrt3}2\\\\~~\boldsymbol{x_1=-\dfrac{\pi}3+2\pi n;~~~x_2=-\dfrac{2\pi}3+2\pi k;~n,k \in \mathbb Z}\\\\2)~\sin x=\dfrac{5\sqrt3+7\sqrt3}4=\dfrac{12\sqrt3}4=3\sqrt3~~>1,~~x\in \varnothing$

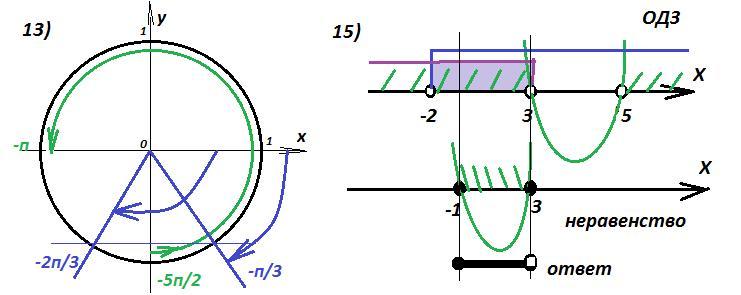
В заданный интервал $\Big[-\dfrac{5\pi}2;-\pi\Big]$ попадает только один корень x₁  при   n=-1 (см. рис)

$x_1=-\dfrac{\pi}3+2\pi\cdot(-1)=-\dfrac{\pi}3-\dfrac{6\pi}3=-\dfrac{7\pi}3$

Ответ : б) $\boldsymbol{x=-\dfrac{7\pi}3}$ ;

а) $\boldsymbol{x_1=-\dfrac{\pi}3+2\pi n;~~~x_2=-\dfrac{2\pi}3+2\pi k;~n,k \in \mathbb Z}$

==========================================

15. В решении НЕЛЬЗЯ умножать неравенство на выражение с переменной, так как неизвестно, какой знак имеет это выражение. При умножении на отрицательное число знак неравенства нужно менять на противоположный. А в данном неравенстве скобка (x+2) находится ПОД логарифмом, это часть аргумента логарифмической функции, избавиться от знаменателя простым умножением невозможно.

$\log_{\frac 13}(18-6x)\leq \log_{\frac 13}(x^2-8x+15)-\log_{\frac 13}(x+2)$

ОДЗ : 1) 18 - 6x > 0;   6x < 18;   x < 3;  x ∈ (-∞; 3)

          2) x + 2 > 0;   x > -2;   x ∈ (-2; +∞)

          3) x² - 8x + 15 > 0;  (x - 5)(x - 3) > 0;   x∈(-∞;3)∪(5;+∞)

ОДЗ : x ∈ (-2; 3)

$\log_{\frac 13}(18-6x)+\log_{\frac 13}(x+2)\leq \log_{\frac 13}(x^2-8x+15)\\\log_{\frac 13}\Big((18-6x)(x+2)\Big)\leq \log_{\frac 13}(x^2-8x+15)\\\\\frac 13<1~~~\Rightarrow~~~(~\leq~\rightarrow~\geq~) \\\\(18-6x)(x+2)\geq x^2-8x+15\\18x-6x^2+36-12x-x^2+8x-15\geq0\\-7x^2+14x+21\geq0~~~~~|:(-7)~\Rightarrow~(~\geq\rightarrow\leq~)\\x^2-2x-3\leq0\\(x-3)(x+1)\leq0\\-1\leq x\leq 3$

С учётом ОДЗ (см. рис):

Ответ : x ∈ [-1; 3)