Предмет: Математика,
автор: WhiteShot
Решить систему уравнений №9
Приложения:

Ответы
Автор ответа:
2
Решение во вложении:
Приложения:
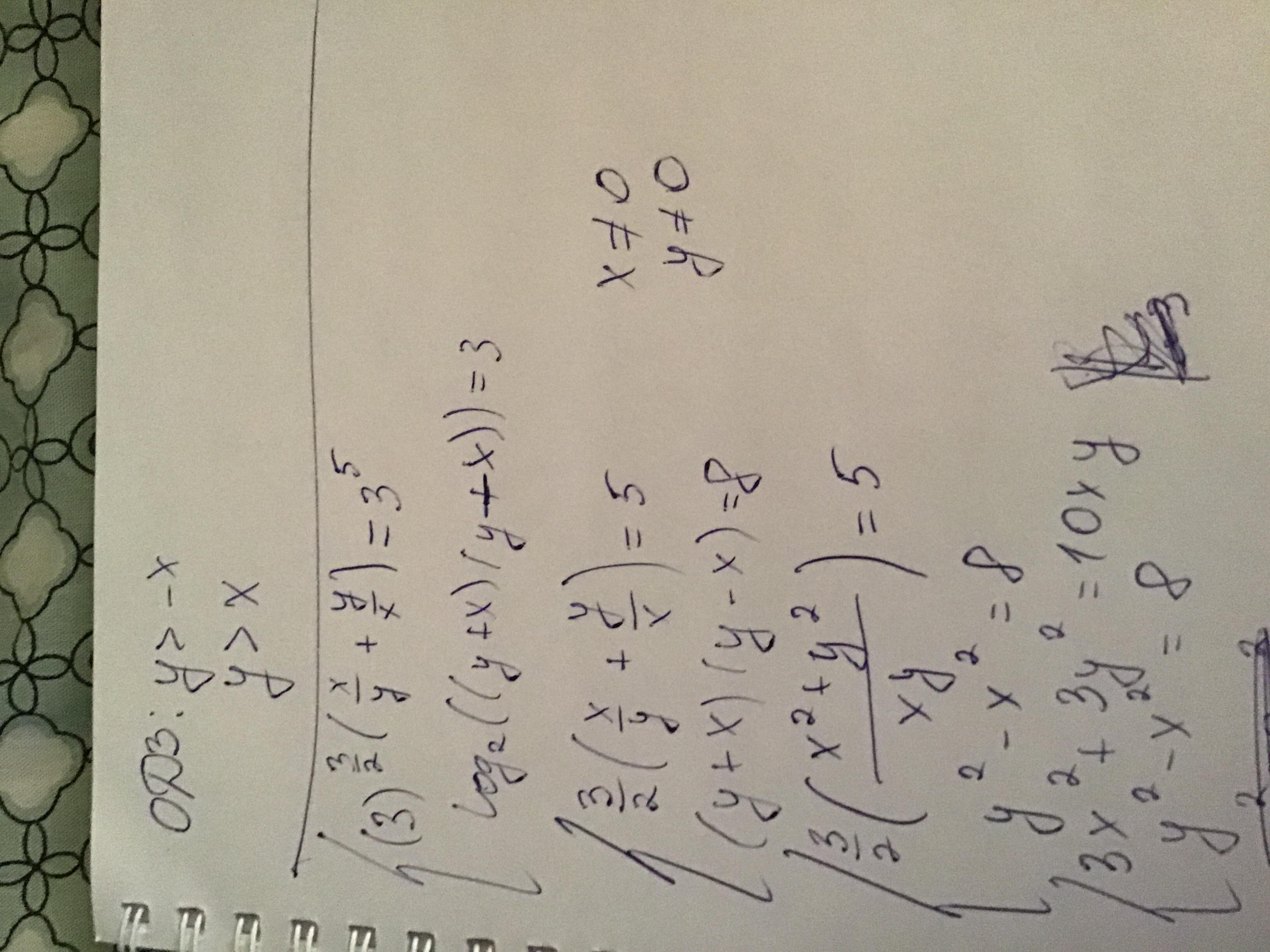

Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: gricenkokata91
Предмет: Английский язык,
автор: hriponukoleksandra
Предмет: Биология,
автор: JoahBAidens
Предмет: Математика,
автор: Алелька3310
Предмет: Математика,
автор: stetsko3006