Предмет: Алгебра,
автор: Evgexa999
срочно! решить неопределенный интеграл с подробным решением, много кто решает и у всех по разному, сделайте точно правильно, пожалуйста
Приложения:
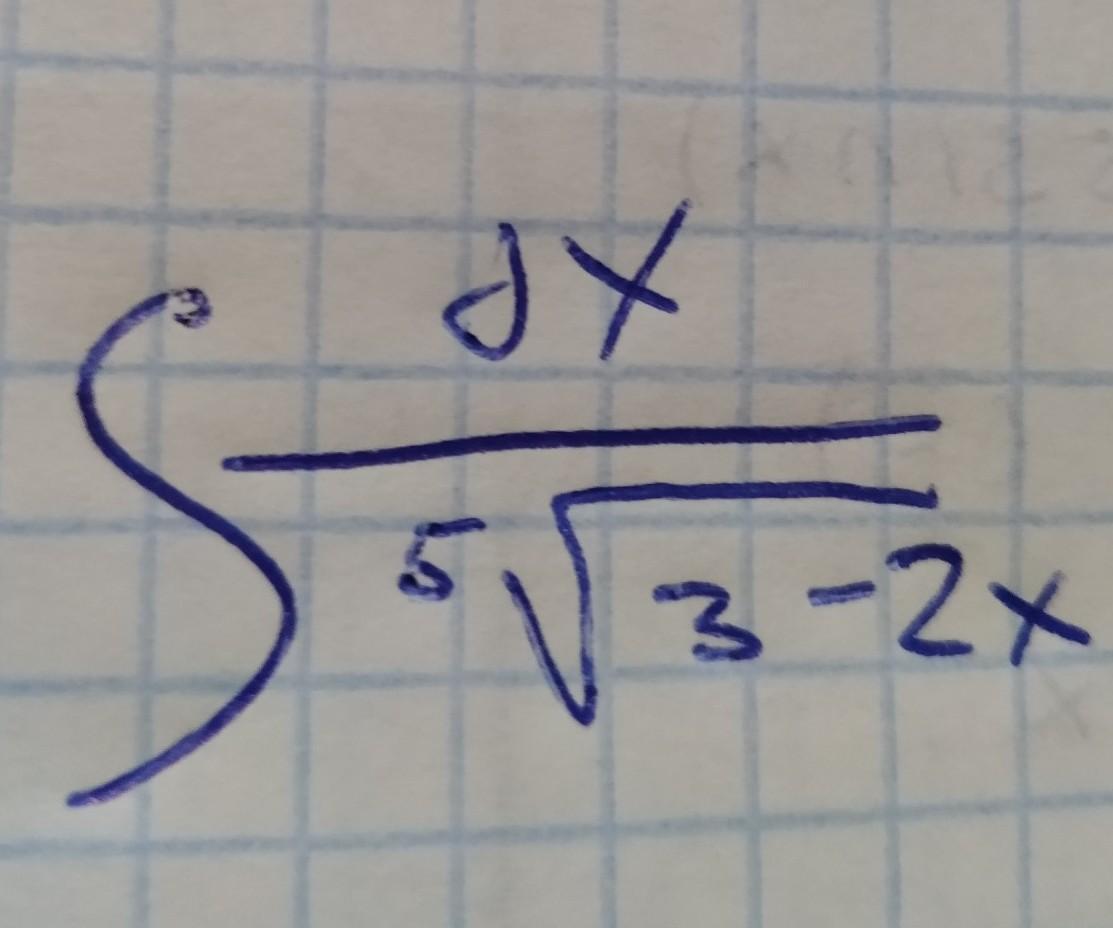
Ответы
Автор ответа:
0
Автор ответа:
1
Преобразуем подынтегральную функцию 1/((3-2х)¹/⁵)=(3-2х)⁻¹/⁵, и с помощью табличного интеграла ∫((ах+b)ⁿ)dx=((ax+b)ⁿ⁺¹)/(a*(n+1))+с, где в нашем случае a=-2; b=3; n=-1/5; с-const;
найдем интеграл ∫dx/((3-2х)¹/⁵)=∫((3-2х)⁻¹/⁵dx=(-1/2)*((3-2х)⁻¹/⁵⁺¹)/((-1/5)+1)+с=
-(5(3-2х)⁴/⁵)/8+с
Проверка. ((-5*(3-2x)⁴/⁵)/8)'=(-4/5) *(5/8)*(3-2x)⁻¹/⁵)*(3-2x)'=(-1/2)*(-2)/((3-2x)¹/⁵)=
1/(3-2x)¹/⁵
Ответ -(5/8)(3-2х)⁴/⁵)+с
Похожие вопросы
Предмет: Английский язык,
автор: barylo2326
Предмет: Биология,
автор: Alevtina3501
Предмет: Физика,
автор: luizats4587
Предмет: Обществознание,
автор: kirodzukat
Предмет: Математика,
автор: Аноним