Предмет: Математика,
автор: maksim88577757
Составить уравнение касательной к графику функции y=x^2-2x, в точке с абсциссой x0=2.выполнить рисунок .
Ответы
Автор ответа:
4
Ответ:
Пошаговое объяснение:
y=x²-2x
y₀=y(x₀)=2²-2*2=0
y'(x)=2x-2
y'(x₀)=y'(2)=2*2-2=2
уравнение касательной
y=y₀+y'(x₀)(x-x₀)
y=2(x-2)
y=2x-4
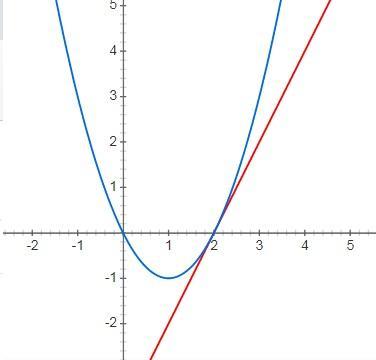
построение
1) y=x²-2x
координаты вершины
х=-b/2a=2/2=1
y(1)=1-2=-1 вершина (1;-1)
точки пересечения с ОХ
у=0 ; x²-2x=0 ; x(x-2)=0 ; x₁=0 ;x₂=2
2) прямая y=2x-4 строим по двум точкам
х=1 у=-2
х=2 у=0
Приложения:
Автор ответа:
4
Дана функция y=x²-2x.
Её производная равна y' = 2x - 2.
В точке х = 2 производная равна y'(2) = 2*2 - 2 = 2.
Функция в точке х = 2 равна у = 2² - 2*2 = 0.
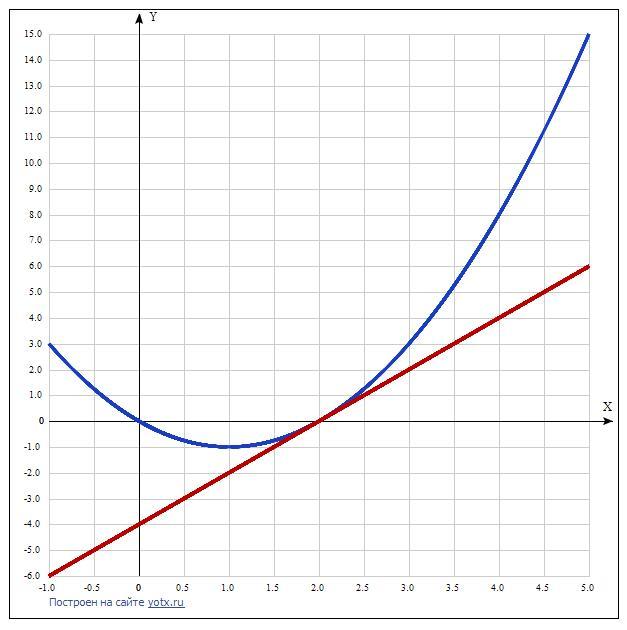
Получаем уравнение касательной в точке х = 2.
у(кас) = y'(х - хо) + у(хо) = 2(х - 2) + 0 = 2х - 4.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: evelinadym
Предмет: Другие предметы,
автор: pcelze244
Предмет: Английский язык,
автор: hfdis9
Предмет: Математика,
автор: OHIBUM