Предмет: Математика,
автор: Hshahajaja
Найти производную сложной функции.картинка прикреплена
Приложения:
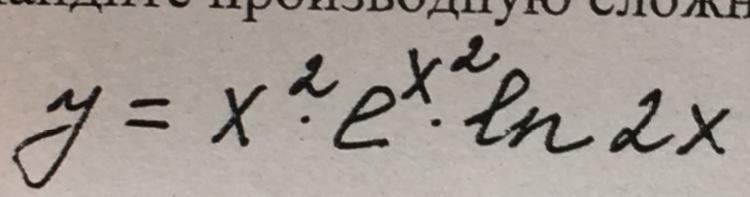
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: bogdanostrovskij676
Предмет: История,
автор: warfpame9
Предмет: Математика,
автор: LVO2021
Предмет: Математика,
автор: nadya1210