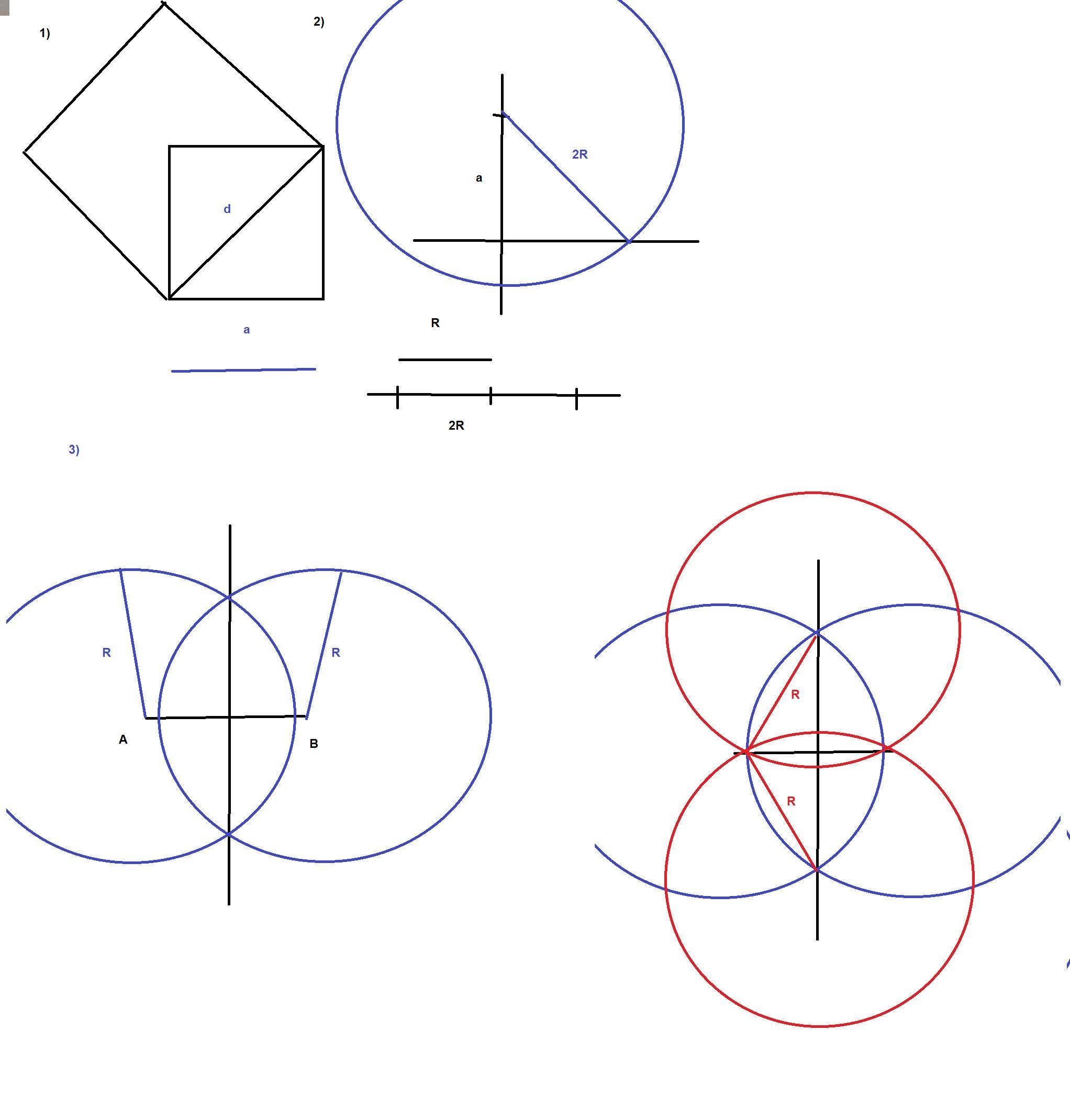Question

8, 9, 10.... пожалуйста помогите!!....срочно
Перевод заданий
8) дано квадрат со стороной а. построить квадрат вдвое большей площади
9) построить прямоугольный треугольник с катетом и радиусом описанной окружности
10) построить круг данного радиуса, проходящей через две данные точки

Answer 1

Объяснение:

8)Смотри. В первом это будет почти невозможно из-за точности наших линеек и тп.

Но возьмём формулу площади S = a^2, => 2S = 2a^2, => Нужно взять сторону sqrt(2)*a

9) Строим отрезок, вдвое больше изначального катета. Дальше иглу циркуля ставим в конец отрезка, стоим окружность, потом не меняя радиуса, ставим в другой конец. В итоге через точки пересечения окружностей мы проводим перпендикуляр, которой ещё  разбивает этот отрезок пополам. Дальше доделываем треугольник. Центр описанной окружности лежит на середине гипотенузы. Находим его середину, как мы раньше проводили перпендикуляр и описываем окружность.

10) Соединяем эти две точки отрезком. Дальше проводим перпендикуляр к этой прямой через середину, как в пункте 9. На этой прямой и лежит центр окружности. Дальше берём нужный нам радиус, грифель ставим в любую из данных точек, а иглу на любую точку на прямой и опысываем окружность.

Answer 2

Ответ:

Объяснение:

решение без описания элементарных построений (серединный перпендикуляр, прямой угол это есть в учебнике)

1) строим квадрат и проводим его диагональ

по теореме Пифагора d²=a²+a²=2a²

значит квадрат со стороной равной диагонали по площади будет в 2 раза больше по площади

2)

так как гипотенуза = 2 радиуса описанной окружности то

строим прямой угол на вертикали откладываем катет

его концы будут вершинами треугольника

из верхней вершины строим окружность радиуса равного двум радиусам описанной окружности ее пересечение с горизонталью это третья вершина

соединяем три вершины

3) соединяем отрезки и строим серединный перпендикуляр

строим две окружности данного радиуса из концов отрезка

из точек пересечения этих окружностей с серединным перпендикуляром строим еще две окружности данного радиуса

получится два круга