Очень очень очень нужна помощь
Ответы
5. находим скорость, дифференцируя функцию, производная равна -2х+7. В точке 3 получим -2*3+7=1
6.значение функции в точке -1 равно 1+1=2, производная функции равна 2х-3х², в точке -1 она равна -2-3=-5, уравнение касательной у равен у в точке минус 1, плюс производная в точке -1, умноженная на (х-(-1))
Подставим. получим у= 2-5*(х+1), или у=-5х-3
7. производная функции равна 3х²-9х. находим критические точки.
3х*(х-3)=0, это ноль и три. Разбиваем обл. опр. этими точками на интервалы и устанавливаем с помощью метода интервалов знаки производной. ______0________3_________
+ - +убывает на отрезке [0;3]; возрастает при х∈ (-∞;0] и при х∈ [3;+∞) .8.Производная равна 6х²-30х+36=6(х²-5х+6)=6(х-2)(х-3), корни нашел по теореме, обратной теореме Виета х=2, х=3, это критич. точки. разбиваем ими на интервалы обл. опр., устанавливаем знаки при переходе через критические точки, получаем ___2_____3_______
+ - +точка х=2 - точка максимума в ней максимум функции равен 16-15*4+36*2-24=4, и минимум в точке минимума х=3, равный 2*27-15*9+36*3-24=54-135+108-24=3
9. критич. точки находим из уравнения 3х²+4х-4=0, это -2 и 2/3. вторая не подходит. находим значения функции в точках -2, 0 в первой точке -8+8+8+4==12, а внуле равна функция 4- это наименьшее значение, наибольшее равно 12.
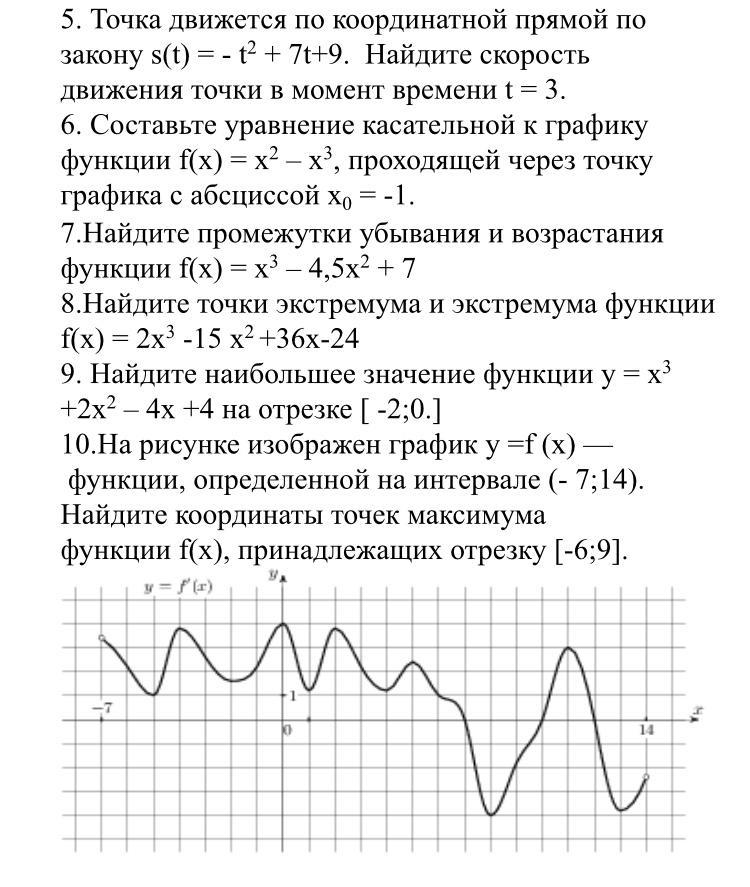
10. это точки(-4;4);(0;4);(2;4);(5;2).