Предмет: Алгебра,
автор: danmadro77
Доказать, что при всех допустимых значениях a справедливо равенство.
Приложения:
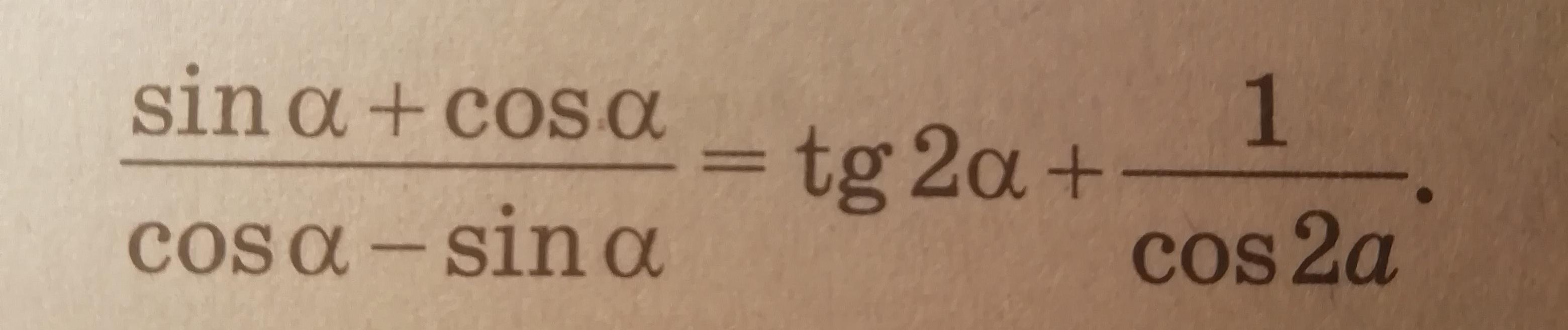
Ответы
Автор ответа:
0
Умножим числитель и знаменатель дроби на cosa + sina, получим:
Автор ответа:
0
Преобразуем правую часть тождества :
Тождество доказано
Похожие вопросы
Предмет: Математика,
автор: smyslovamilana5810
Предмет: Информатика,
автор: juliakosobokova24
Предмет: Биология,
автор: danielsel
Предмет: Математика,
автор: animal302
Предмет: Литература,
автор: лоло60