ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА!!!!!!!!
№1 Найдите точки экстремума функции: f(x)=12x-x^3+2
№2 Прямоугольник вращается вокруг меньшей стороны.Найти площадь полной поверхности полученого тела вращения,если диагональ равна 12 см,а угол между диагональю и меньшей стороной прямоугольника равна 60 градусов.
Ответы
Ответ:
1) x=±2
2) 678,24+226,08√3≈1069,22
Пошаговое объяснение:
1) Точки экстремума - точки, в которых производная обращается в 0 и, проходя через которые, меняет свой знак.
Найдём производную: f'(x)=12-3x^2
Приравняем к 0: 12-3x^2=0
4-x^2=0
x^2-4=0
x=±2
Это и есть точки экстремумов функции
2) Фигура вращения прямоугольника вокруг стороны a с оставшейся стороной b - цилиндр с высотой a и радиусом b.
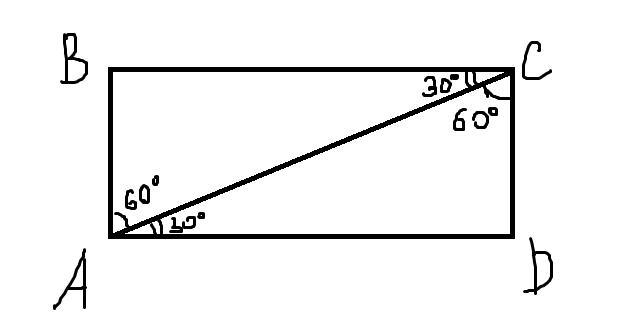
Чертёж прилагается. ∠ACD=60° => ∠CAD=30° => по свойству катета, лежащего против угла в 30°, CD=AC/2=12/2=6 => по теореме Пифагора AD==
=6√3
S=2πr(r+h)=2*3,14*6√3(6√3+6)=678,24+226,08√3≈1069,22
1. Прежде найдем производную. она равна 12-3х², далее найдем критические точки. 12-3х²=0, х²=4; х=±2, установим с помощью метода интервалов знаки производной при переходе через критич. точки.
____-2_____2_____
- + -
Точка х=-2 - точка минимума, т.к. при переходе через нее производная меняет знак с минуса на плюс, а точка х=2 - точка максимума, т.к. меняет производная знак с плюса на минус. Эти точки и есть точки экстремума.
2.Угол между диагональю и большей стороной равен 30°, поэтому меньшая сторона равна половине диагонали 12/2=6, это высота цилиндра -фигуры вращения прямоугольника вокруг меньшей стороны , а радиус его основания равен большей стороне 12*sin60° =12*√3/2=6√3
S=2πR(R+h)=2*π*6√3(6√3+6)=(216+72√3)π/см²/