Предмет: Математика,
автор: vasiq141
Вывести cos (a-b) !!!!!!
Ответы
Автор ответа:
0
Для начала введём единичную окружность и отметим углы α и β, α > β. Отметим также векторы a и b, которые образуют углы α и β соответственно.
Вспомним, что скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, а этот угол равняется α-β. Длины этих векторов равны 1, так как являются радиусами единичной окружности, а произведение этих векторов в координатах равно . Но мы знаем, что x – это косинус угла, а y – синус. Тогда
. Заменив x и y на косинусы и синусы, получим известную формулу косинуса разности.
Приложения:
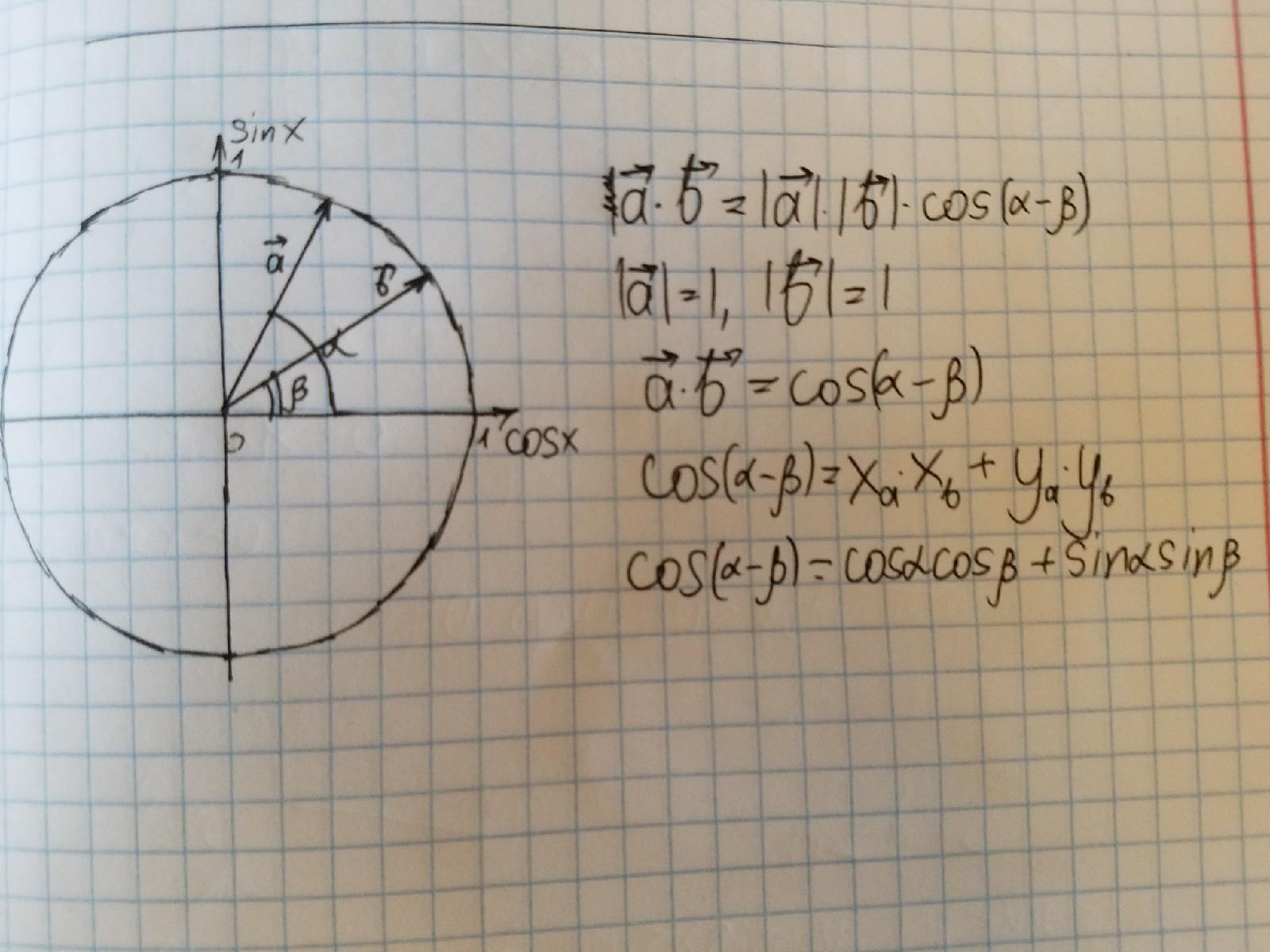
Автор ответа:
0
Доказательство во вложении :
Приложения:


vasiq141:
спасибо
Похожие вопросы
Предмет: История,
автор: artemmakisev71
Предмет: Математика,
автор: Kris20094
Предмет: Математика,
автор: aishakichikova
Предмет: Алгебра,
автор: XeniaArynova