Question

q(x)=x⁵- 5x³ исследовал при помощи производной и построить график функций

Answer 1

$Q(x)=x^5-5x^3$

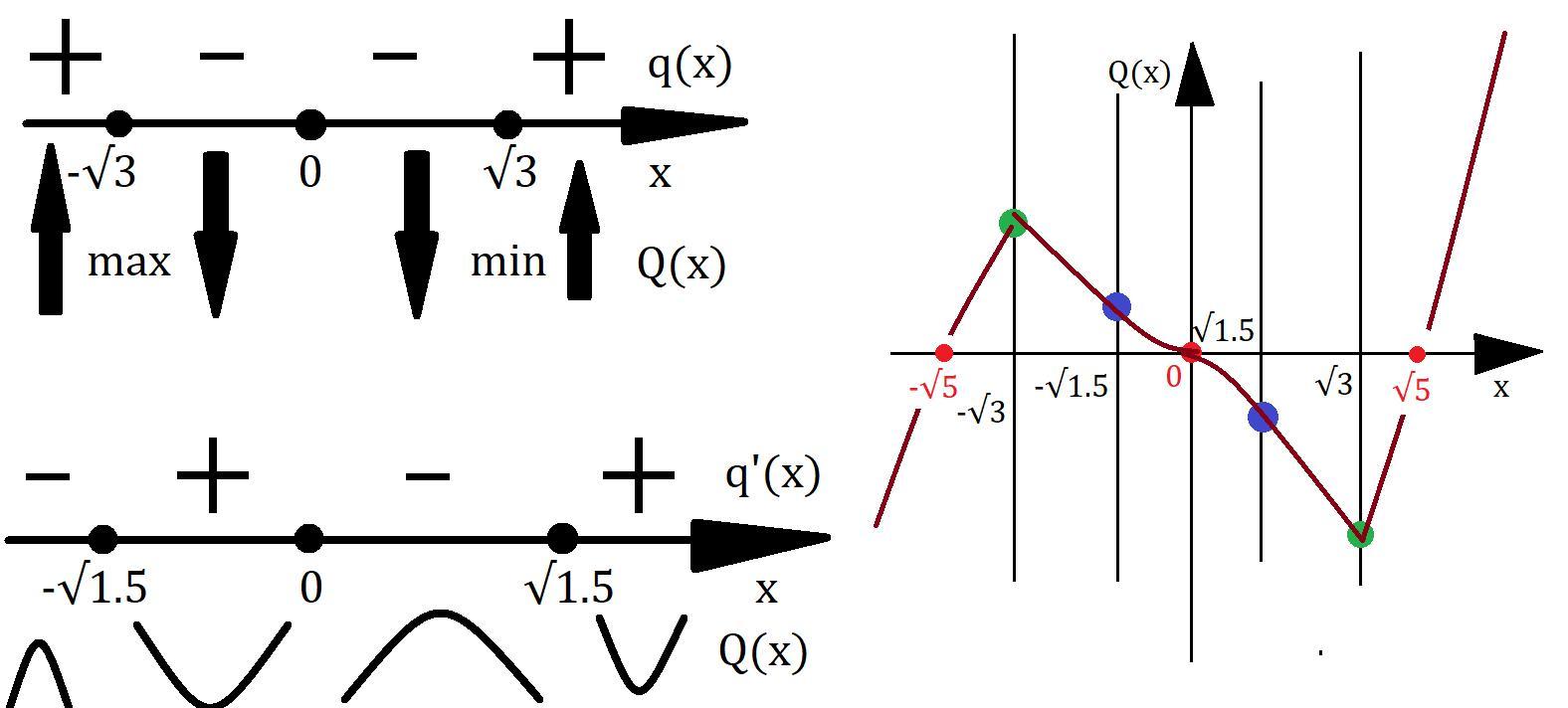
Для начала найдём точки пересечения с осями координат.

$Q(0)=0^5-5*0^3=0,(0;0)\\Q(x)=x^5-5x^3=x^3(x^2-5)=0\\(-\sqrt{5};0),(0;0),(\sqrt{5};0)$

Функция нечётная т.к. Q(x)= -Q(-x)

Исследуем функцию на возрастание, убывание и экстремумы.

$Q'(x)=q(x)=5x^4-15x^2=5x^2(x^2-3)=\\5x^2(x-\sqrt{3})(x+\sqrt{3})\\Q(0)=0\\Q(-\sqrt{3})=-9\sqrt{3}+15\sqrt{3}=6\sqrt{3}\\Q(\sqrt{3})=-6\sqrt{3}$

Смотри вниз.

Исследуем функцию на выпуклость вверх, вниз и точки перегиба.

$Q''(x)=q'(x)=20x^3-30x=20x(x^2-1.5)=\\x(x-\sqrt{1.5})(x+\sqrt{1.5})\\Q(0)=0\\Q(-\sqrt{1.5})=-\frac{9}{4}\sqrt{1.5}+\frac{15}{2}\sqrt{1.5}=\frac{21}{4}\sqrt{1.5}\\Q(\sqrt{1.5})=-\frac{21}{4}\sqrt{1.5}$

Смотри вниз.

$6\sqrt{3}V\frac{21}{4}\sqrt{1.5};24^2*3V21^2*1.5;576>147*1.5$

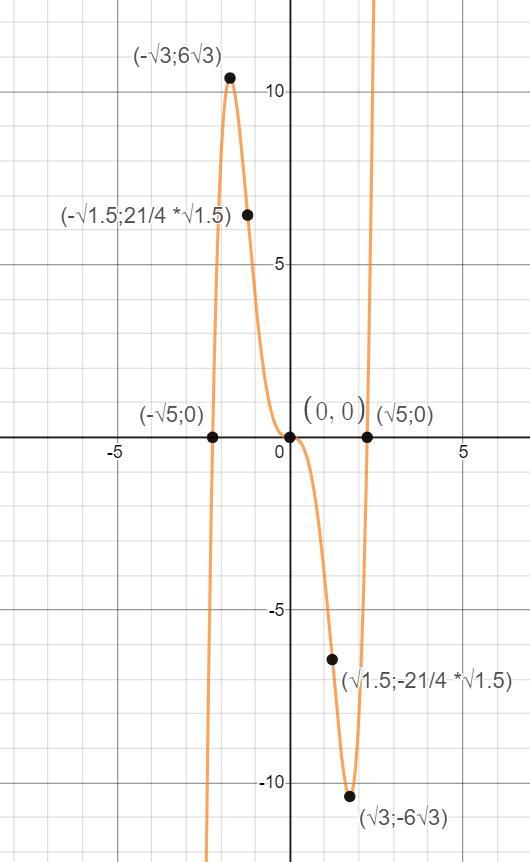
У нас есть всё, чтобы построить график функции.