Предмет: Алгебра,
автор: ovruk333
Интегралы (98 баллов)
Приложения:
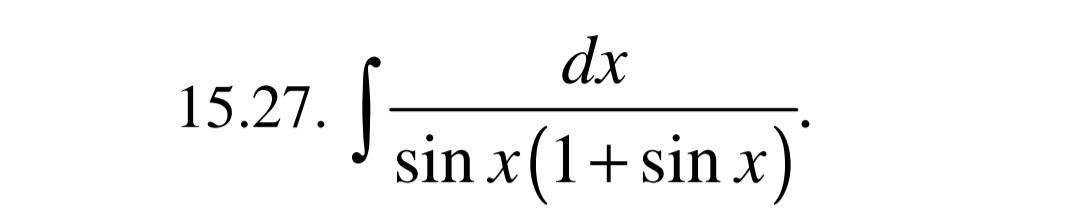
mathgenius:
Проще всего через основную тригонометрическую подстановку. Хотя можно и по другому
Ответы
Автор ответа:
0
Ответ: ln(tg(x/2))+2/(1+tg(x/2) )+c
Объяснение:
Преобразуем знаменатель подынтегральной функции:
sin(x)*(1+sin(x) ) = 2*sin(x/2)*cos(x/2)* (sin(x/2)+cos(x/2) )^2=
=2*cos^4(x/2)*tg(x/2) *(1+tg(x/2))^2
dx/(sin(x) *(1+sin(x) ))= dx/(cos^2(x/2) )/2*cos^2(x/2)*tg(x/2)*(1+tg(x/2))^2
cos^2(x/2)+sin^2(x/2)=1
1+tg^2(x/2)=1/cos^2(x/2)
int( (1+tg^2(x/2))*d(tg(x/2))/ ( tg(x/2)*(1+tg(x/2))^2) )
tg(x/2)=t
int( (1+t^2)*dt/t*(1+t)^2)
(1+t^2)/(t*(t+1)^2) = ( (t+1)^2-2t)/(t*(t+1)^2) =1/t -2/(1+t)^2
int( (1+t^2)*dt/t*(1+t)^2)=int( (1/t -2/(1+t)^2)dt)= ln(t)+2/(1+t)+c= ln(tg(x/2))+2/(1+tg(x/2) )+c
Похожие вопросы
Предмет: Українська мова,
автор: solomiyazheliasko
Предмет: Русский язык,
автор: marinearakeljan
Предмет: Алгебра,
автор: serzanbahitzan
Предмет: Литература,
автор: ProStoYlitka