Question

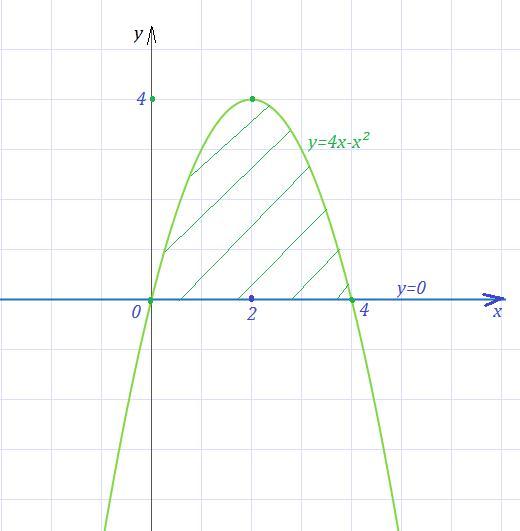
Прошу помочь найти площадь фигуры,ограниченной линиями y=4x-x^2,y=0

Answer 1

найдем пределы интегрирования, решив уравнение. 4х-х²=0, х=0; х=4

По формуле Ньютона- Лейбница  найдем определенный интеграл от нуля до четырех от разности 4х-х²-0, получим 2х²-х³/3, подставим пределы интегрирования. 2*16-64/3-0+0=32-21целая 1/3=10 целых 2/3

Answer 2

$y=4x-x^2\; \; ,\; \; y=0\\\\4x-x^2=0\; ,\; \; x(4-x)=0\; \; \to \; \; x_1=0\; ,\; x_2=4\\\\S=\int\limits^4_0\, (4x-x^2)\, dx=(4\cdot \frac{x^2}{2}-\frac{x^3}{3})\Big |_0^4=2\cdot 16-\frac{64}{3}=32-\frac{64}{3}=\frac{32}{3}=10\frac{2}{3}$