Предмет: Алгебра,
автор: zalenskayaolia
помогите решить уравнения
Приложения:
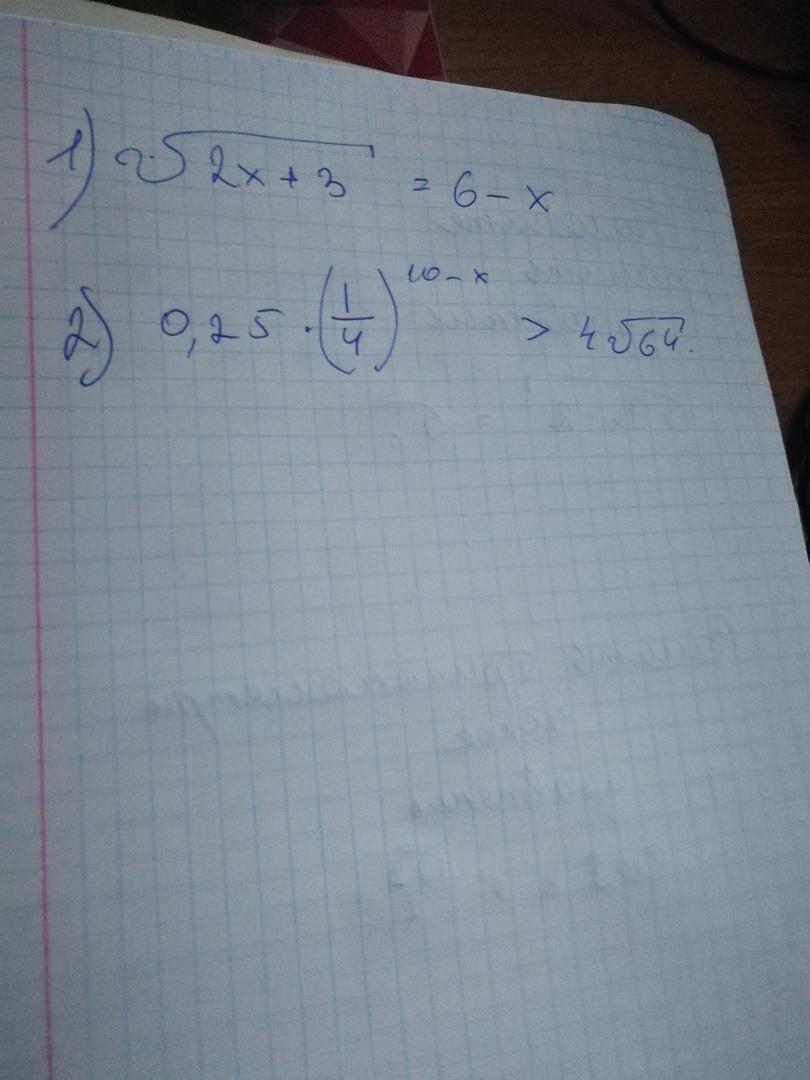
Ответы
Автор ответа:
3
1)
2)
Автор ответа:
1
1.возведем в квадрат обе части уравнения 2х+3=36-12х+х²; х²-14х+33=0, По теореме, обратной теореме Виета х=3, х=11, проверка.
√(2*3+3)=6-3;3=3- верно, х=3- корень уравнения.
х=11; √(22+3)=6-11; 5=-5 не верно. х=11 - не корень уравнения.
2. 0.25=1/4=2⁻², поэтому 2⁻²*2⁻²*⁽¹⁰⁻ˣ⁾>2²*2³; при умножении степеней с одинаковыми основаниями показатели складываются. поэтому -22+2х>5, откуда 2х>27, х>27/2; x>13.5
Похожие вопросы
Предмет: Математика,
автор: dariasira856
Предмет: Музыка,
автор: primachenkoiaroslav
Предмет: Физика,
автор: cvb115
Предмет: Математика,
автор: lolololol22
Предмет: Математика,
автор: angel1233451528