Question

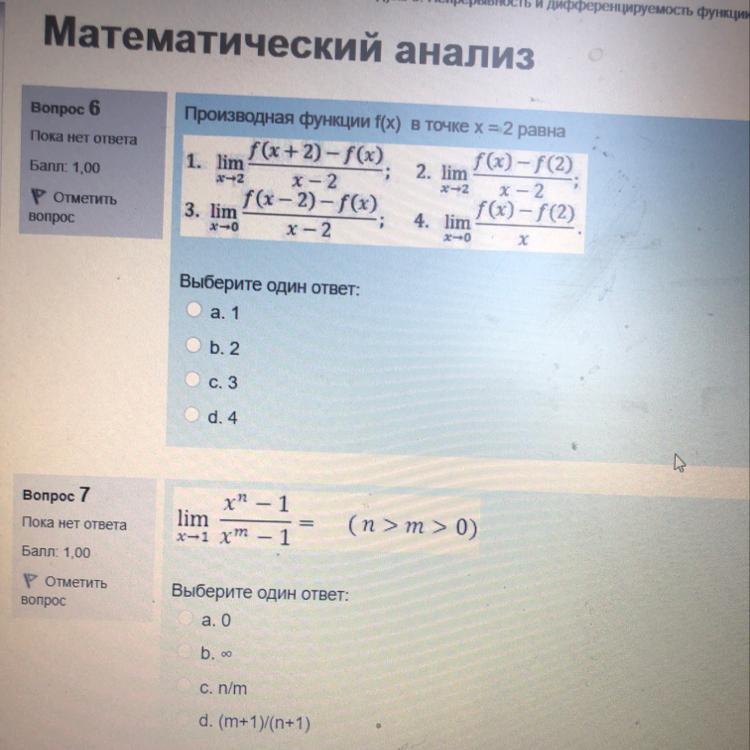
Выбрать один вариант ответа на вопрос 6 и 7

Answer 1

Ответ:6. b. 2

7.  c. n/m

Пошаговое объяснение:

6. Применяем формулу производной функции

$f'(x_o) =lim_{x \to\ x_o} \frac{f(x)-f(x_o)}{x-x_o}}$

При х₀=2 формула примет вид

$f'(2) =lim_{x \to\ 2} \frac{f(x)-f(2)}{x-2}}$

что соответствует ответу b. 2

7. При вычислении предела для раскрытия неопределенности 0/0 применяем правило Лопиталя

$\lim_{x \to k} \frac{f(x)}{g(x)}=\lim_{x \to k} \frac{f'(x)}{g'(x)}$

$\lim_{x \to 1} \frac{x^n-1}{x^m-1}=\lim_{x \to 1} \frac{(x^n-1)'}{(x^m-1)'}=\lim_{x \to 1} \frac{nx^{n-1}}{mx^{m-1}}=\lim_{x \to 1} \frac{nx^{n-m}}{m}=\frac{n}{m}$

что соответствует ответу c. n/m

Answer 2

6.

При х₀=2 формула примет вид ответа b. 2

По определению производной, это предел отношения приращения функции к приращению аргумента, причем последний стремится к нулю.

7. При вычислении предела для раскрытия неопределенности 0/0 применяем правило Лопиталя и получаем ответ c. n/m