Помогите решить пожалуйста! даю 100 баллов;)
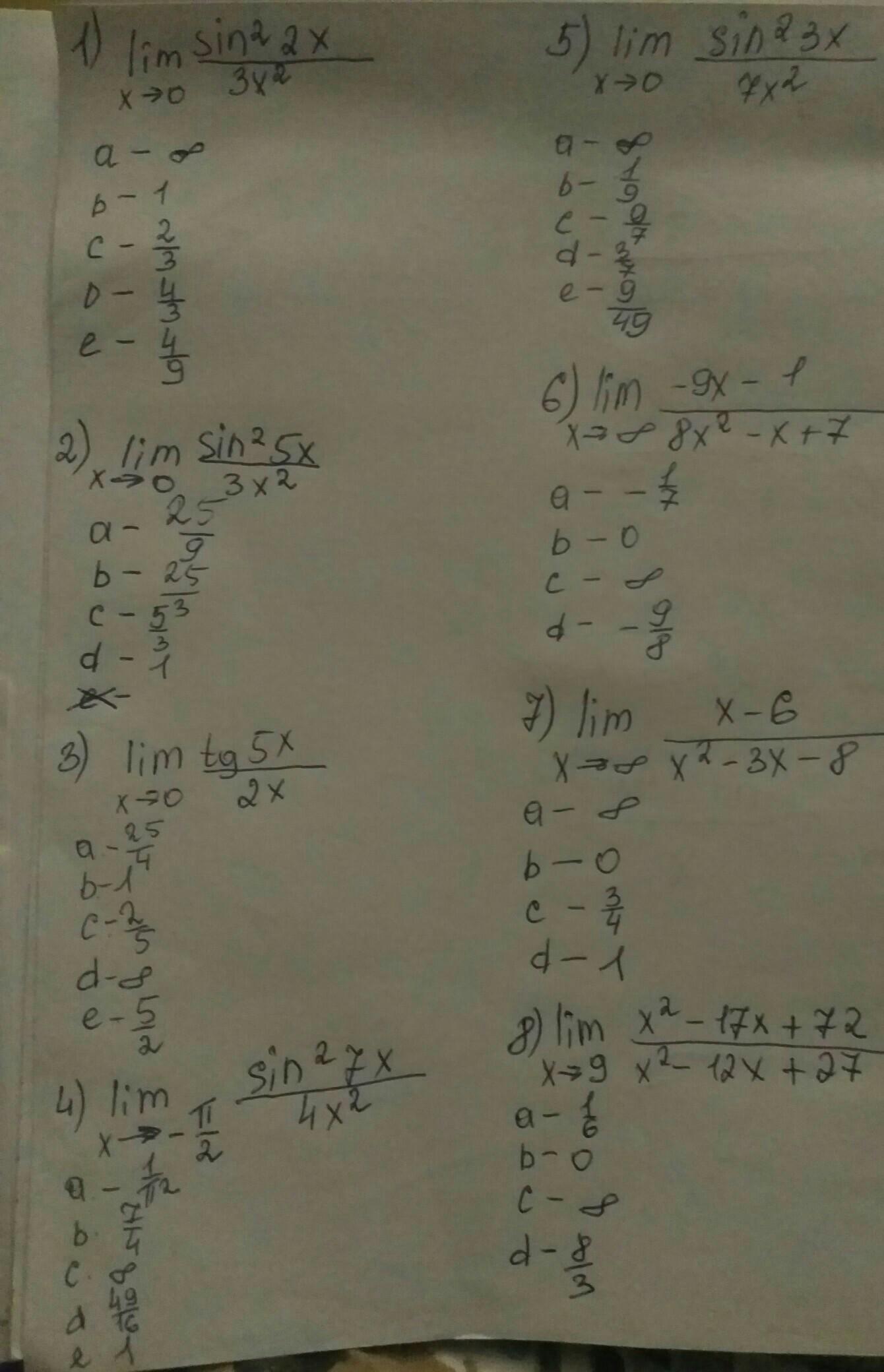
Ответы
Ответ:
Объяснение:
==============

1. Примеры 1, 2, 3, 5 на применение первого замечат. предела, предел отношения синуса икс к иксу, при икс стремящемся к нулю равен единице. Поэтому в пятом примере предел эквивалентен пределу отношения (9*3х*3х)/(7*3х*3х))=9/7; ответ С) ;во втором домножаем числитель и знаменатель на 25, получаем (25*5х*5х)/(3*5х*5х)=25/3, ответ В); в первом расписываем синус в квадрате как (синус 2х)*(синус 2х) и домножаем числитель и знаменатель на 4, получаем предел отношения
(4*2х*2х)/(3*2х*2х)=4/3, ответ Д); в третьем тангенс эквивалентен 5х, поэтому имеем предел отношения (5х/2х)=5/2, ответ Е);
в четвертом примере надо просто подставить данные, получим отношение (синуса в квадрате (-7π/2))/(4*π²/4)=1/π², ответ А), да, еще здесь синус от (-7π/2)=(-синус 7π/2)=(-синус (2π+3π/2))=(-синус(3π/2))=1, да в квадрате, тоже 1.
6-7 тоже однотипны. Правило такое, если числитель и знаменатель многочлены стандартного вида, а икс стремится к бесконечности, то сразу можно писать ответом плюс бесконечность, если степень числителя выше степени знаменателя, а если наоборот, то ответ нуль, и если показатели степеней одинаковые, то ответом будет частное от деления коэффициента старшей степени числителя на старшую степень знаменателя, т .е. в 6. это будет ноль, ответ В), а в 7 примере тоже ноль, т.к. степень числителя 1, а знаменателя 2. Ответ В). И наконец, 8. Числитель раскладывается как (х-9)*(х-8), а знаменатель, как (х-9)*(х-3), после сокращения и подстановки получим 1/6, ответ А) УДАЧИ!