Предмет: Математика,
автор: monolit75mail
Помогите решить!!!!!!!
Приложения:
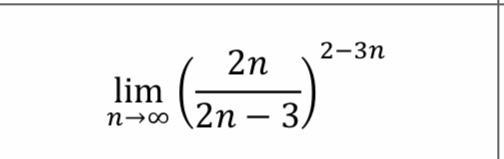
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Геометрия,
автор: artemion123
Предмет: Другие предметы,
автор: panchenkosonya84
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: сафия22
Предмет: Математика,
автор: полинка202пл