помогите, пожалуйста, исследовать функцию производной и подробно описать
Я просто не понимаю(
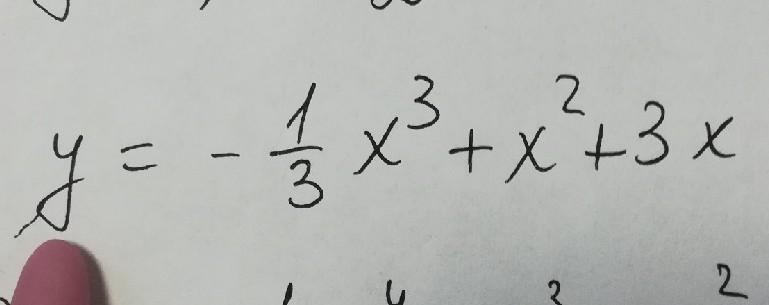
Ответы
Ответ:
Пошаговое объяснение:
y'=-x^2+2x+3 =0, корни x1=-1, x2=3, на числовой прямой отмечаем эти критические точки и знаки производной, ____-1_____ 3_____
, знаки вверху - + - , в точке -1 min, в точке 3 max, функция убывает при x<=-1 и x>=3, и возрастает -1<=x<=3, y=0 при х=0,
находим значения ф-ции в точках -1 и 3, у(-1)=1/3+1-3=-1 1/3
у(3)=-1/3*27+9+9=9, обл.опр-я (-~; +~), обл. знач. (-~; +~)
найдем производную, она равна -x²+2x+3; Найдем критические точки функции, решив уравнение. -x²+2x+3 =0, корни уравнения x₁=-1, x₂=3, на числовой прямой отмечаем критические точки и знаки производной, решая неравенство, например, (х+1)(х-3)>0, находя одновременно и положительные и отрицательные значения производной, с помощью метода интервалов, нанося на ось критические точки рассматривая знаки производной, где она положительна, там функция возрастает, где отрицательна убывает, а точка, в которой производная меняет знак с минуса на плюс, это точка минимума, с плюса на минус - точка максимума. ЭТО точки экстремума, а сами экстремумы получим, когда подставим эти точки в функцию. Итак ____-1_____ 3_____
- + -
в точке х= -1 min, равный 1/3+1-3=-1 целая 2/3, в точке х=3 max, равный -9+9+9=9; функция убывает при x∈(-∞;-1] и x∈[3;+∞) и возрастает при х∈ [-1;3], y=0 при х=0,
Область определения и область значения (-∞;+∞)